Question 1118244: Compare 10^2 and 2^10. For any two numbers make a conjucture about which usually gives the greater number, as the base or as the exponent.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Compare 10^2 and 2^10. For any two numbers make a conjucture about which usually gives the greater number, as the base or as the exponent.
~~~~~~~~~~~~~~~~~~
I'd like to answer the second question of this post.
For any two numbers make a conjecture about which usually gives the greater number, as the base or as the exponent.
So, the question is: if x and y are two positive numbers and y > x, what is greater, 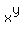 or or 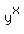 ? ?
The answer is: if both x and y are greater than "e" and x < y, then 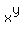 > > 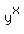 . (*) . (*)
In wording form: if in the domain x, y > e you raise the smaller number to the greater degree, you will get the greater number
than if you raise the greater number to the smaller degree.
Solution
Let's start from this inequality
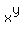 > > 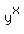 . (1)
Take the logarithm from both sides. You will get
y*ln(x) > x*ln(y). (2)
Divide both sides by the product ln(x)*ln(y). You will get . (1)
Take the logarithm from both sides. You will get
y*ln(x) > x*ln(y). (2)
Divide both sides by the product ln(x)*ln(y). You will get
 > > 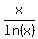 . (3) <<<---=== in the domain x, y > e you are safe to do it . . .
Now the KEY STATEMENT is that the inequality (3) is TRUE (!).
Why it is true ? - Because the function F(x) = . (3) <<<---=== in the domain x, y > e you are safe to do it . . .
Now the KEY STATEMENT is that the inequality (3) is TRUE (!).
Why it is true ? - Because the function F(x) = 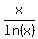 monotonically increases as x increases in the domain x > e.
I will not prove the last statement.
Everybody who is familiar with Calculus, can easily do it on his or her own.
Which is better, I will demonstrate this fact visually, by presenting the plot: monotonically increases as x increases in the domain x > e.
I will not prove the last statement.
Everybody who is familiar with Calculus, can easily do it on his or her own.
Which is better, I will demonstrate this fact visually, by presenting the plot:
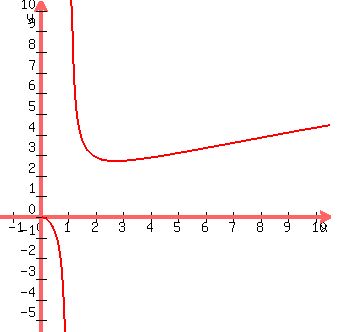 Plot y =
Plot y = 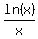 Now, if you reverse the arguments in this sequence (3) ----> (2) ----> (1), you will get the major statement (*) proved.
Now, if you reverse the arguments in this sequence (3) ----> (2) ----> (1), you will get the major statement (*) proved.
-----------------
So, to the popular question - which number is greater,  or or  , the answer is: , the answer is:  is greater than is greater than  . .
|
|
|