Question 1118220: Brian buses tables at a local cafe. To bus a table, he must clear the dirty dishes and reset the table for the next set of customers. One night he noticed that for every three-fifths of a table that he bused, another table of customers would get up and leave. He also noticed that right after he finished busing a table, a new table of customers would come into the restaurant. However, once every table was empty (no diners were left in the restaurant), nobody else came into the restaurant. Suppose there were six tables with customers and one unbused table. How many new tables of customers would come in before the restaurant was empty? After the last table of customers had left, how many tables were unbused?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! When  sets of customers had left the cafe sets of customers had left the cafe
(  sets who where seating at their tables initially, sets who where seating at their tables initially,
and  sets who entered and left the cafe), sets who entered and left the cafe),
Brian has bused  tables, tables,
so  new tables of customers had come in, new tables of customers had come in,
and Brian rushed to lock the door before an 8th set of customers could come in.
At that point the number of unbused tables was
 . .
STEPWISE:
As Brian has bused  of a table, of a table,  table-ful of customers leaves, so now Brian has table-ful of customers leaves, so now Brian has  more table to bus, more table to bus,
to be added to the  left to do of the table he is busing. left to do of the table he is busing.
For each set of customers that leaves the restaurant,
the number of tables unbused increases by 
(compared to the number unbused when the previous set of customers left).
As Brian has bused  tables, tables,  table-ful of customers have left, table-ful of customers have left,
but at the same time new customers have filled  tables. tables.
The number of tables in use has decreased by  as as  tables emptied. tables emptied.
As Brian has bused  tables, tables, 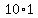 table-ful of customers have left, table-ful of customers have left,
but at the same time new customers have filled  tables, tables,
leaving  tables occupied. tables occupied.
After that,  more table-fuls of diners will have to leave for the cafe to be empty, more table-fuls of diners will have to leave for the cafe to be empty,
because by the time the customers in those  occupied tables leave, occupied tables leave,
Brian will have bused  table, table,
but as he finished busing one table, another table became occupied.
As the last  table-fuls of customers left, table-fuls of customers left,
a total of  table-fuls of customers had left, table-fuls of customers had left,
Brian had bused  tables, tables,
while the number of tables to be bused had increased by  , ,
so after Brian locked the door, the number of unbused tables was
 . .
|
|
|