SOLUTION: Use De Moivres Theorem to show which integral powers of {{{ (-1+i)/(sqrt (2)) }}} are real, and which are imaginary.

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Use De Moivres Theorem to show which integral powers of {{{ (-1+i)/(sqrt (2)) }}} are real, and which are imaginary.      Log On


   

Question 1118160: Use De Moivres Theorem to show which integral powers of 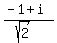+%28-1%2Bi%29%2F%28sqrt+%282%29%29+ are real, and which are imaginary.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Integral powers of 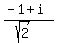+%28-1%2Bi%29%2F%28sqrt+%282%29%29 are real
if the integer exponent is a multiple of 4 ( such as 0,4,8,..., or -4,-8, -12,...).
They are imaginary if the integer exponent is a multiple of 2, but not a multiple of 4
(such as 2,6,10,..., or -2,-6,-10,...).


If p is an integer,
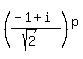
+%28%28-1%2Bi%29%2F%28sqrt+%282%29%29%29%5Ep%22=%22%22%5B%22cos%28pi%2F4%29%2Bi%2Asin%28pi%2F4%29%22%5D%22%5Ep%22=%22cos%28p%2Api%2F4%29%2Bi%2Asin%28p%2Api%2F4%29
will be real if sin%28p%2Api%2F4%29=0 ,
and will be imaginary if cos%28p%2Api%2F4%29=0 .

sin%28p%2Api%2F4%29=0 if and only if p%2Api%2F4=k%2Api for some integer k ,
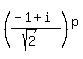That means That the integral power +%28%28-1%2Bi%29%2F%28sqrt+%282%29%29%29%5Ep is real only if and only if
p is a multiple of 4.

cos%28p%2Api%2F4%29=0 if and only if p%2Api%2F4=k%2Api%2Bpi%2F2=%28%282k%2B1%29%2F2%29%2Api for some integer k ,
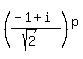That means That the integral power +%28%28-1%2Bi%29%2F%28sqrt+%282%29%29%29%5Ep is imaginary if and only if, for some integer k ,
p%2F4=%282k%2B1%29%2F2 <--> p=4k%2B2 ,
which means p is even, but not a multiple of 4.