Question 1118158: A bag contains 10 red, 8 green and 7 blue balls, If two balls are picked at random one after the other without replacement from the bag, what is the probability that:
(i) they are of the different colors
(ii) at least a ball is blue?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
A bag contains 10 red, 8 green and 7 blue balls, If two balls are picked at random one after the other
without replacement from the bag, what is the probability that:
(i) they are of the different colors
The favorable sets are (R,G) or (R,B) or (G,B).
Correspondingly, the probability under the question is
P =  +  +  .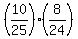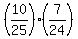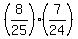
Here 25 = 10 + 8 + 7 is the total number of balls and 24 = 25-1.
You may complete it as a fraction or use your calculator to get the decimal number.
(ii) at least  one ball is blue?
The favorable sets are (R,B) or (G,B) or (B,B).
Correspondingly, the probability under the question is
P = + +  .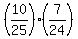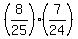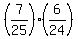
You may complete it as a fraction or use your calculator to get the decimal number.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
There are many ways to calculate probabilities like these.
Basically, you want to put the worded requirements in terms of ANDs and/or ORs and then, in your calculations, replace each AND with a multiplication and each OR with an addition.
You can count the number of ways of getting the desired outcome and get the probability by dividing by the total number of ways of choosing 2 of the 25 balls, which is C(25,2) = 300.
Or you can think of drawing one ball at a time and work with the probability of good outcomes on each draw.
Following are a few ways you could do the second problem.
(1) Find the number of ways of choosing 2 of the 7 blue balls AND none of the 18 other colors OR 1 of the 7 blue balls AND 1 of the other 18 balls:
Then the probability is 147/300.
(2) Find the probability of choosing a blue ball AND then another blue ball, OR choosing a blue ball AND then a different color ball, OR choosing a different color ball and then a blue ball:
(3) Find the number of ways of choosing 2 balls which are both NOT blue; convert that number to a probability, and subtract from 1:
 ; 
(4) Find the probability of choosing a ball that is not blue AND then another ball that is not blue, and subtract that from 1:
I would strongly recommend that you try solving problems like this in at least a couple of different ways. Seeing that you can use different methods to get the same right answer gives you confidence in the work you are doing.
I will just note a couple of ways you can work the first problem, using methods similar to those above.
(1) Find the number of ways of choosing 1 red AND 1 blue OR 1 red AND 1 green OR 1 blue AND 1 green; add and convert to a probability by dividing by 300.
(2) Find the number of ways of getting 1 red AND 1 of either other color OR of getting 1 blue AND 1 green; convert to a probability as in the other method.
(3) Find the probability of getting a blue AND then a different color, OR getting a red AND then a different color, OR getting a green AND then a different color.
(4) Find the probability of getting 2 blue OR 2 red OR 2 green and subtract from 1.
|
|
|
