SOLUTION: The ratio of the interior angle to the exterior angle of a regular polygon is 5 : 2. Find the number of sides of the polygon.

According to the condition, the interior angle is 5x, while the exterior angle is 2x,

where x is (an unknown) common measure of the two angles.



Since interior and exterior angles are supplementary, you have

2x + 5x = 180 degrees,  or  7x = 180 degrees,  i.e.  x = 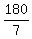.    (1)



Next, the sum of exterior angles is 360 degrees:

n*(2x) = 360 degrees,  or  n = 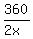.    (2)



Substitute here x = 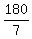 from (2). You will get

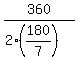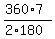n =  =  = 7.


Answer.  The number of sides of the polygon is 7.