Question 1118089: https://vle.mathswatch.co.uk/images/questions/question16415.png
please help
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's look at the four cases:
Let P(R,R) = probability of selecting red then another red
What value is P(R,R)?
On the first pick, there are 7 red and 11 total, so P(R) = 7/11
On the 2nd pick, there are 6 red and 10 total, so P(R,R) = (7/11)*(6/10) = 42/110
1. P(R,R) = 42/110
Similarly, using W for white:
2. P(R,W) = (7/11)*(4/10) = 28/110
3. P(W,R) = (4/11)*(7/10) = 28/110
4. P(W,W) = (4/11)*(3/10) = 12/110
Notice these cover all possible outcomes, as expected. We know this because the numerators, when added, sum to 110 and 110/110=1
The probability of one of each color is just the sum of case 2, P(R,W), and case 3, P(W,R):
28/110 + 28/110 = 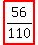 or about 0.51 or about 0.51
I hope this helps you.
|
|
|