SOLUTION: sketch the graph of y=3+|x-2|clearly stating your arguments. what is the range of the function?

Algebra ->  Absolute-value -> SOLUTION: sketch the graph of y=3+|x-2|clearly stating your arguments. what is the range of the function?      Log On


   

Question 1117647: sketch the graph of y=3+|x-2|clearly stating your arguments. what is the range of the function?
Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39623) About Me  (Show Source):
You can put this solution on YOUR website!
Minimum y is 3.
At (2,3) for minimum point.

Range is y%3E=3.


graph%28300%2C300%2C-7%2C7%2C-7%2C7%2C3%2Babs%28x-2%29%29

Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


The response from the other tutor was rather brief, and may not be much help to you if you are having trouble understanding the problem....

An absolute value is always 0 or positive. So the minimum value of abs%28x-2%29 is 0; and that value is obtained when x-2=0 --> x+=+2.

So in your function, 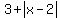3%2Babs%28x-2%29, the minimum value is when x=2; and at x=2 the function value is 3%2Babs%282-2%29+=+3%2Babs%280%29+=+3%2B0+=+3.

So the turning point ("vertex") of the graph is at (2,3).

For values of x less than 2, x-2 is negative, so abs%28x-2%29+=+2-x, and the equation is y+=+3%2B2-x or y+=+-x%2B5; that line has a slope of -1.

For values of x greater than 2, x-2 is positive, so abs%28x-2%29+=+x-2, and the equation is y+=+3%2Bx-2 or y+=+x%2B1; that line has a slope of +1.

So the minimum value of the function is at (2,3) and from that point the graph to the right has a slope of +1 and the graph to the left has a slope of -1.

Clearly the lower end of the range of the function is y=3. And there is nothing to keep the value of y getting larger "forever"; so the range of the function is from 3 to infinity.