SOLUTION: expand (1+2x)(1-x)^6 as far as the term in x^4 and use it to evaluate 1.06*(0.97)^6. correct to 4 decimal places. find the value of R in the coefficient of the Rth term from beg

Algebra ->  Finance -> SOLUTION: expand (1+2x)(1-x)^6 as far as the term in x^4 and use it to evaluate 1.06*(0.97)^6. correct to 4 decimal places. find the value of R in the coefficient of the Rth term from beg      Log On


   

Question 1117632: expand (1+2x)(1-x)^6 as far as the term in x^4 and use it to evaluate 1.06*(0.97)^6. correct to 4 decimal places.
find the value of R in the coefficient of the Rth term from beginning and the Rth term from the end of the expansion of (3x+5)^15 are in the ratio of 27:125
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


1st question...

Use Pascal's Triangle to expand %281-x%29%5E6:

%281-x%29%5E6+=+1-6x%2B15x%5E2-20x%5E3%2B15x%5E4 plus other terms that we aren't using

Then

%281%2B2x%29%281-x%29%5E6 =
%281%2B2x%29%281-6x%2B15x%5E2-20x%5E3%2B15x%5E4%29 =
1-4x%2B3x%5E2%2B10x%5E3-25x%5E4%2B30x%5E5

Substituting x=.03, we get



The actual value of %281.06%29%280.97%29%5E6 is 0.8829503252 to 10 decimal places. The approximation agrees with the actual value to 6 decimal places.

Rounded to 4 decimal places the approximation is the same as the actual value.

-------------------------------------------
2nd question....

Again thinking of using the binomial coefficients in Pascal's Triangle to solve this problem, we know that the R-th binomial coefficient from the beginning of the row and the R-th one from the end of the row are the same.

So, when we are finding the ratio of the coefficients, we can ignore that part of the calculation; the ratio of the two coefficients will just be

%28%283%29%5En%2A%285%29%5E%2815-n%29%29%2F%28%283%29%5E%2815-n%29%2A%285%29%5En%29

We want this ratio to be 27%2F125+=+3%5E3%2F5%5E3

So



Then

2n-15+=+3
2n+=+18
n+=+9

So the ratio of the coefficients of the x^9 and x^6 terms will be 27/125.

I'm not sure how that translates to the answer to the question that was asked. The x^9 term is the 7th term in the expansion if the powers are in descending order; but I don't know if you call that the 6th term from the beginning or the 7th term from the beginning.

-------------------------------------------------------

Added in response to reader's comment "answer is 7 can you try once more"....

The way the question is worded is not clear. What does "the R-th term from the beginning" mean? Is the 7th term in an expression the 7th term from the beginning or the 6th term from the beginning? (The 7th term in an arithmetic sequence is 6 terms after the first....)

In my original response I worked the problem and said that R was either 6 or 7, depending on how you interpreted the question.

So if you know the answer is supposed to be 7, then my solution is complete and correct. There is no need for me to "try once more".

Answer by ikleyn(52852) About Me  (Show Source):
You can put this solution on YOUR website!
.

I will answer the second question only,  but to begin with,  I reformulate it in more accurate way  (hope you agree with it) 

    find the value of R highlight%28cross%28in%29%29 if the coefficient of the Rth term from beginning and the Rth term from the end 
    of the expansion of (3x+5)^15 are in the ratio of 27:125

Solution 

The binomial expansion is this formula


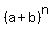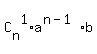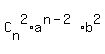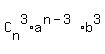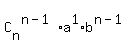%28a%2Bb%29%5En = a%5En + C%5Bn%5D%5E1%2Aa%5E%28n-1%29%2Ab + C%5Bn%5D%5E2%2Aa%5E%28n-2%29%2Ab%5E2 + C%5Bn%5D%5E3%2Aa%5E%28n-3%29%2Ab%5E3 + . . . + C%5Bn%5D%5E%28n-1%29%2Aa%5E1%2Ab%5E%28n-1%29 + b%5En


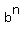In our case,  n = 15,  a = 3x,  b = 5,  therefore, the binomial expansion in our case is  


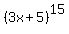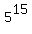%283x+%2B+5%29%5E15 = %283x%29%5E15 + C%5B15%5D%5E1%2A%283x%29%5E14%2A5 + C%5B15%5D%5E2%2A%283x%29%5E13%2A5%5E2 + C%5B15%5D%5E3%2A%283x%29%5E12%2A5%5E3 + . . . + C%5B15%5D%5E14%2A%283x%29%2A5%5E14 + 5%5E15.


Let R = (k+1)     (or, which is the same,  k = R-1).


The R-th term from the beginning is  C%5B15%5D%5Ek%2A%283x%29%5E%2815-k%29%2A5%5Ek,  k = 0, 1, 2, . . . , 14.

The R-th term from the end       is  C%5B15%5D%5E%2815-k%29%2A%283x%29%5Ek%2A5%5E%2815-k%29,  k = 0, 1, 2, . . . , 14.


Calculating the ratio of these coefficients, we can cancel the binomial coefficients, since they have the same value.  Now the ratio


R_th_term_from_the_beginning%2FR_th_term+_from_the_end = %283%5E%2815-k%29%2A5%5Ek%29%2F%283%5Ek%2A5%5E%2815-k%29%29 = 3%5E%2815-2k%29%2F5%5E%2815-2k%29,


and we want this ratio would be equal to  3%5E3%2F5%5E3.


It means  15-2k = 3  ====>  15-3 = 2k  ====>  12 = 2k  ====>  k = 12%2F2 = 6.


Answer.  k= 6, which means  "the 7-th term of the binomial expansion from the beginning" :  R = k+1 = 7.


There was an error in calculations by  @greenestamps,  which I fixed in my solution.