Question 1117621: A hand of 5 cards is dealt from a standard deck
How many hands with 2 king and 3 clubs are possible?
Found 2 solutions by josmiceli, greenestamps:
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! Order is not important, so this is a problem
using combinations, not permutations
Number of hands = C( 3,2 ) * C( 12,3 )
C( 3,2 ) =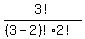 
C( 3,2 ) = 
C( 3,2 ) =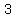 
and
C( 12,3 ) =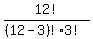 
C( 12,3 ) = 
C( 12,3 ) = 
C( 12,3 ) =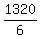 
C( 12,3 ) =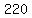 
------------------------
C( 4,2 )*C( 13,3 ) =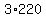 
There are 660 possible hands
Note that one of the kings counted is a club, so that
won't work, and one of the clubs being counted is a king
and that won't work either, so I need to account for them
Feel free to get another opinion on this
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
The king of clubs can not be one of the cards. If it were, then "2 kings and 3 clubs" would be only 4 cards; but the problem says 5 cards were dealt.
So the hands we are considering are those that contain 2 of the 3 kings that are not clubs and 3 of the 12 clubs that are not kings.
So the answer from the other tutor is correct:
|
|
|
