SOLUTION: In the expansion of (1+x)^n, the coefficient of x^5 is the arithmetic mean of the coefficients of x^4 and x^6. calculate the possible values of n

Algebra ->  Statistics  -> Binomial-probability -> SOLUTION: In the expansion of (1+x)^n, the coefficient of x^5 is the arithmetic mean of the coefficients of x^4 and x^6. calculate the possible values of n      Log On


   

Question 1117570: In the expansion of (1+x)^n, the coefficient of x^5 is the arithmetic mean of the coefficients of x^4 and x^6. calculate the possible values of n
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13214) About Me  (Show Source):
You can put this solution on YOUR website!


The coefficients are....

C(n,4) = 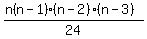%28n%28n-1%29%28n-2%29%28n-3%29%29%2F24

C(n,5) = %28n%28n-1%29%28n-2%29%28n-3%29%28n-4%29%29%2F120

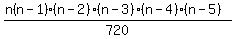
C(n,6) = %28n%28n-1%29%28n-2%29%28n-3%29%28n-4%29%28n-5%29%29%2F720

We need to find the value(s) of n for which C(n,5) is the arithmetic mean of C(n,4) and C(n,6).

An interesting problem; but the algebra works out relatively easily....



Multiply by the common denominator 1440 and cancel the common factors n through n-3:

12%28n-4%29+=+30%2B%28n-4%29%28n-5%29
12n-48+=+30%2Bn%5E2-9n%2B20
n%5E2-21n%2B98+=+0
%28n-7%29%28n-14%29+=+0

The two solutions are n=7 and n=14.

Check:

For n=7, the coefficients are 7, 21, and 35; 21 = (7+35)/2.

For n=14, the coefficients are 1001, 2002, and 3003; 2002 = (1001+3003)/2.

DONE!

Answer by ikleyn(52898) About Me  (Show Source):
You can put this solution on YOUR website!
.
The binomial expansion of  %281%2Bx%29%5En  is this formula


%281%2Bx%29%5En = 1%5En + C%5Bn%5D%5E1%2A1%5E%28n-1%29%2Ax + C%5Bn%5D%5E2%2A1%5E%28n-2%29%2Ax%5E2 + C%5Bn%5D%5E3%2A1%5E%28n-3%29%2Ax%5E3 + . . . + C%5Bn%5D%5E%28n-1%29%2A1%5E1%2Ax%5E%28n-1%29 + x%5En,

or, which is the same

%281%2Bx%29%5En = 1 + C%5Bn%5D%5E1%2Ax + C%5Bn%5D%5E2%2Ax%5E2 + C%5Bn%5D%5E3%2Ax%5E3 + . . . + C%5Bn%5D%5E%28n-1%29%2Ax%5E%28n-1%29 + x%5En.



    coefficient at x^5  is   C%5Bn%5D%5E5 = n%21%2F%28%28n-5%29%21%2A5%21%29;

    coefficient at x^4  is   C%5Bn%5D%5E4 = n%21%2F%28%28n-4%29%21%2A4%21%29;

    coefficient at x^6  is   C%5Bn%5D%5E6 = n%21%2F%28%28n-6%29%21%2A6%21%29.



The equation for the three coefficients is


    C%5Bn%5D%5E5 = %281%2F2%29%2A%28C%5Bn%5D%5E4+%2B+C%5Bn%5D%5E6%29,   or


    n%21%2F%28%28n-5%29%21%2A5%21%29 = %281%2F2%29%2A%28n%21%2F%28%28n-4%29%21%2A4%21%29+%2B+n%21%2F%28%28n-6%29%21%2A6%21%29%29%29.


In both sides, cancel common factors  n!,  (n-6)! and 4!.  You will get

    1%2F%28%28n-5%29%2A5%29 = %281%2F2%29%2A%281%2F%28%28n-5%29%2A%28n-4%29%29+%2B+1%2F%285%2A6%29%29.


Multiply both sides by  2*(n-5)*(n-4)*5*6.  You will get, step by step

    2*(n-4)*6 = 5*6 + (n-5)*(n-4)

    12*(n-4)  = 30  + n^2 - 9n + 20

    12n - 48  = n^2 - 9n + 50

    n^2 - 21n + 98 = 0

     (n-14)*(n-7) = 0.


The roots are  n= 7  and  n= 14.


Check.  n= 7  ====>  C%5B7%5D%5E5 = 21;  C%5B7%5D%5E4 = 35;  C%5B7%5D%5E6 = 7;   21 = 0.5*(35+7)   ! Correct !


        n= 14  ====>  C%5B14%5D%5E5 = 2002;  C%5B14%5D%5E4 = 1001;  C%5B14%5D%5E6 = 3003;   2002 = 0.5*(1001+3003)   ! Correct !

Solved.