Question 1117492: A multiple-choice quiz has 15 questions, each with 4 possible answers of which only 1 is the correct answer. What is the probability that a student gets at least 1 correct answer?
Answer by ikleyn(52887)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. The basic space of events has  elements.
Each element of this set is the word of the length 15 with 4 possible letters/symbols in each of 15 positions.
You can consider these letters as A, B, C and D, symbolizing the possible answer option on each of 15 questions.
In other terms, the basic space of events is the set of the words of the length 15 over the alphabet consisting of 4 letters/symbols.
2. In each of 15 positions, there is only one "correct" symbol, symbolizing the correct answer.
Other 3 symbols in each position correspond to incorrect answers.
Thus the set of "unwanted" events has elements.
Each element of this set is the word of the length 15 with 4 possible letters/symbols in each of 15 positions.
You can consider these letters as A, B, C and D, symbolizing the possible answer option on each of 15 questions.
In other terms, the basic space of events is the set of the words of the length 15 over the alphabet consisting of 4 letters/symbols.
2. In each of 15 positions, there is only one "correct" symbol, symbolizing the correct answer.
Other 3 symbols in each position correspond to incorrect answers.
Thus the set of "unwanted" events has  elements.
Each element is 15-letter word, which has one of the three "incorrect" answers in each of the 15 position.
3. Therefore, the probability to have ALL incorrect answers to each of 15 questions is elements.
Each element is 15-letter word, which has one of the three "incorrect" answers in each of the 15 position.
3. Therefore, the probability to have ALL incorrect answers to each of 15 questions is
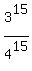 = = 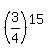 = =  = 0.013363 . . .
while the probability to get at least 1 correct answer is = 0.013363 . . .
while the probability to get at least 1 correct answer is
 - - 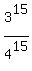 = = 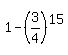 = = 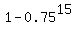 = 1 - 0.013363 = 0.986637 . . . , or 98.66%. = 1 - 0.013363 = 0.986637 . . . , or 98.66%.
Answer. The probability under the question is 0.9866, or 98/66%.
|
|
|