SOLUTION: A rancher wishes to create 4000 square meter rectangle enclosure. Two fences parallel to two of the sides will be used to create three equal areas. Find the dimensions of the fence

Let the enclosure dimensions be  x = length, y = width, so the area is xy = 4000 square meters.


Then you have a rectangle of the perimeter of 2x + 2y plus two additional fence parts of the length y. 


The total length of the fencing with two additional fence parts is 2x + 4y meters.


Thus you need to minimize  2x + 4y  under the condition  xy = 4000.


Express y = 4000/x  and substitute it into  2x + 4y.  Then you will get that the function to minimize is  .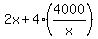


To find a minimum, differentiate the function over x and equate to zero. 


So, the equation for the minimum is


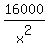 -  = 0,   or  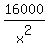 = 2  ====>   =  = 8000  ====>  x =  = .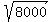


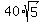Thus the optimal dimensions are: the length = 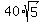 = 89.44 m  and

                                 the width =  =  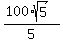=  = 44.72 m.


Check.  89.44*44.72 = 4000 square meters.   ! Correct !