SOLUTION: Without using L'Hospitals rule find : Limt((e^(17x)-17e^x +16)/(e^(16x)-16e^x+15)). as x=0

Introduce  z = .  Then the given fraction takes the form

    fraction = .    (1)



The polynomial    has the root z=1  and therefore is divided by (z-1) without a remainder.

The factoring formula is  

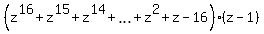 = .     (2)



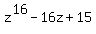Similarly, the polynomial    has the root z=1  and therefore is divided by (z-1) without a remainder.

The factoring formula is  

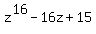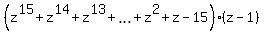 = .     (3)



If you substitute (2) and (3)  into (1), you will get after canceling (z-1)

    fraction =     (4)


It is still not a safe situation, since both polynomials in numerator and denominator of (4) have z= 1 as a root.


So, we need divide each of (2) and (3) by (z-1) one more time. If you do it, you will get

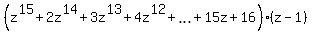 = ,   (5)

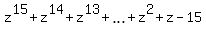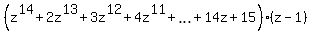 = .   (6)



Hence, when you substitute (5) and (6) into (4) and cancel the common factor (z-1) again, you will get

    fraction =    (7)


Now you can safely find the limit of (7) at z ---> 1  simply substituting z = 1 into its numerator and denominator. You will get

    fraction limit at z --> 1 is equal to  =    (8)


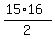Easy summation of arithmetic progressions gives  Numerator =  = 136,  Denominator =  = 120.


Hence the answer is:  The given fraction limit at x ---> 0 is    = .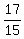