You can
put this solution on YOUR website! .
Let x be the rate on the first river.
Your "time" equation is
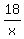 +
+ 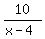 = 8 hours.
It is "time" equation, because each fraction in the left side represents the time traveled on corresponding river.
To solve it, multiply both sides by x*(x-4). You will get a quadratic equation.
Simplify it and solve it by any method you know/(you like).
The answer is x= 6 kilometers per hour. (I solved it mentally).
= 8 hours.
It is "time" equation, because each fraction in the left side represents the time traveled on corresponding river.
To solve it, multiply both sides by x*(x-4). You will get a quadratic equation.
Simplify it and solve it by any method you know/(you like).
The answer is x= 6 kilometers per hour. (I solved it mentally).