Question 1117080: Water is being poured at the rate of 2pi cubic meter per minute into an inverted conical tank that is 12 m deep with the radius of 6 m at the top. If the water level is rising at the rate of 1/6 m/min and there is a leak at the bottom of the tank, how fast is the water leaking when the water is 6-m deep?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the conical tank, with radius  and height and height  , ,
 <--> <-->  . .
Whatever the water level, the water in the tank is a cone
similar in shape to the tank itself, with  . .
The volume of water in the tank when the water id  m deep is m deep is
 , ,
with  in m and in m and  in in  . .
The volume in the tank increases at a rate, in 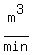 of of
 . .
When the water depth is  , ,  , ,
and the rate of water volume increase, in 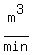 , is , is
 . .
With water entering the tank at  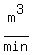 , ,
and water leaking out at an unknown rate of  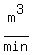 , ,
the water volume is increasing at a rate of  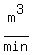 . .
That means that
 --> --> 
When the water depth is 6m, water is leaking at  cubic meters per minute. cubic meters per minute.
|
|
|