Question 1117037: This is an extra credit question for a topic very briefly touched on in class.
A step by step explanation would be extremely helpful due to not having a full lesson in this. (but know that would be time consuming!)
Graph at least two full periods of the following function. Label the 5 key points on one period. Give the amplitude and period of the function.. y=-2sin(2x)
there is an
x y empty chart for 5 points. (I assume 0, pi/2, pi, 3pi/2, and 2pi)
also a black graph to draw the function
Any help would be greatly appreciated, but it is extra credit- so not necessary!
Found 2 solutions by stanbon, Alan3354:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Graph at least two full periods of the following function. Label the 5 key points on one period. Give the amplitude and period of the function.. y=-2sin(2x)
there is an
x y empty chart for 5 points. (I assume 0, pi/2, pi, 3pi/2, and 2pi)
----
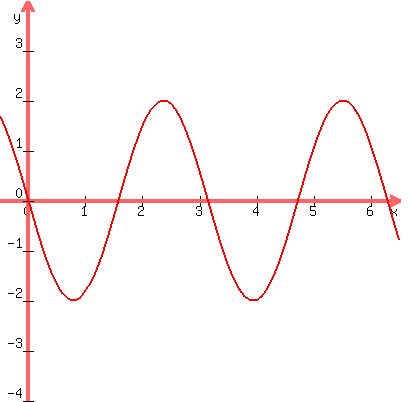
f(x) = -2sin(2x)
f(0) = -2*sin(0) = 0
f(pi/2) = -2sin(2(pi/2)) = -2sin(pi) = 0
f(pi) = -2sin(2*pi) = 0
f(3pi/2) = -2sin(2(3pi/2) = -2sin(3pi) = 0
f(2pi) = -2sin(4pi) = 0
----
amplitude = |-2| = 2
period = (2pi)/2 = pi radians
Cheers,
Stan H.
--------------
Answer by Alan3354(69443)  (Show Source):
|
|
|
