Question 1116990: If tan (A+B)= x and tan B =1/2 prove that tan A=2x-1/x+2 and obtain an expression in terms of x. If tan (A-B)=1/3 and A is acute ,find without using tables.
My solution:
On using tan(A+B) formula
X=(tan A +1/2)/1-tan.1/2
X=[(2tan A+1)/2]/1-tanA/2
X=[(2tan A+1)/2)]/(2-tan A)/2
X=(2tan A+1/2)*2/2-tan A
X=2tan A+1/2-tan A
2x-x tan A=2tan A +1
2x-1=2tan A+tan A
2x-1/2-x=tan A
And I have got
tan(A-B)= 3x-4/4x+3
Third part I am not getting please explain me
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! As posted, it is a very puzzling problem.
THE PUZZLING LAST QUESTION:
After much reading and re-reading,
I believe the last part of the problem asks you to first find
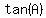  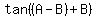 knowing knowing  and and  . .
That should be easy for you,
since you obviously know how to use the trigonometric identity for tangent of a sum of angles.
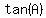  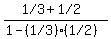  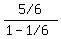  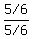  . .
At that point, I believe you may also be expected to figure out
that if  and and  is an acute angle, is an acute angle,
then  (or (or  if you are expected to express it in radians. if you are expected to express it in radians.
What puzzled me most is the phrase "without using tables".
In 7th grade, I was taught to use a small, pocket "table of logarithms" book
to find values of logarithms and trigonometric functions,
but that was 55 years ago. Ten years later we were all buying expensive Hewlett Packard or Texas Instruments calculators that could do that and little else. Nowadays we can buy cheap calculators that can do that and much more.
Does anyone use tables any more? Or is that a vintage problem that teachers have been assigning for half a century or longer?
REGARDING THE REST OF THE PROBLEM:
If tan (A+B)= x and tan B =1/2 ,
I can prove that tan A=(2x-1)/(x+2)= , ,
which I believe is what you tried to write,
although some very necessary parentheses were missing,
and some mischievous imp turned a + into a - at the end of your proof.
If I am then asked to find an expression in terms of  , ,
I ask "an expression for what?"
If I am told what is required is an expression for 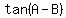 , ,
I would come up with tan(A-B)=(3x-4)/(4x+3)}}}
as you undoubtedly wrote on paper.
NOTE/RANT:
When typing, you need to type a lot of parentheses.
Paper and pencil writing lets you save effort with a long horizontal line
that implies parentheses wrapping the expressions above and below the line.
Your work, except for lack of parentheses and that - sign , is flawless,
but if you type a calculation into a modern calculator without necessary parentheses,
I bet the calculator will follow order of operation conventions and give you the right answer to your wrong question.
At work, I once saw a chemist make that mistake and report on the phone the nonsense result from the screen of the calculator, as I was frantically shaking my head. Years later, we were still called the group that could not calculate their way out of a paper bag.
Answer by ikleyn(52848)   (Show Source): (Show Source):
|
|
|