Question 1116963: if angle is in Quadrant II, express the remaining trigonometric functions in terms of sin(angle).
Found 2 solutions by Theo, Alan3354:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if your angle is in quadrant 2, then:
sine is positive.
cosine is negative.
tangent is negative because it is sine / cosine = positive / negative = negative.
cosecant is reciprocal of sine, therefore also positive.
secant is reciprocal of cosine, therefore also negative.
cotangent is reciprocal of tangent, therefore also negative.
here's a reference on the sign of the trigonometric functions in each quadrant.
http://www.sparknotes.com/math/trigonometry/trigonometricfunctions/section3/
the rules are summarized another way below:
sine is positive in first and second quadrant.
cosine is positive in first and fourth quadrant.
tangent is positive in first and third quadrant.
sine is negative in third and fourth quadrant.
cosine is negative in second and third quadrant.
tangent is negative in second and fourth quadrant.
it all has to do with the unit circle, which is used to display the angles in each quadrant and to find their associated trigonometric functions.
the radius of this unit circle is equal to 1.
the horizontal sides of the angles formed are on the x-axis.
the vertical sides of the angles formed are parallel to the y-axis.
becauwe the radius of the circle is also the hypotenuse of the triangles formed, then the length of the hypotenuse of the triangles formed is always equal to 1.
this results in the sine funtion always being equal to y and the cosine function always being equal to x.
for example:
sine of angle = y/h.
since h = 1, then sine of angle = y.
cosine of angle = x/h.
since h = 1, then cosine of angle = x.
the sine function is positive when y is positive which is when y is above the x-axis.
the cosine function is positive when x is positive which is when x is to the right of the y-axis.
the tangent function is positive when x and y are both positive or when x and y are both negative.
here's my picture that should help you see what i mean.
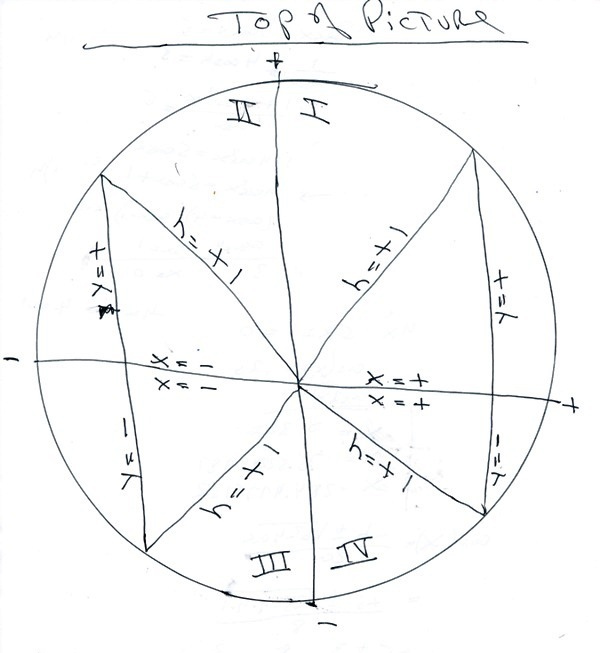
h = hypotenuse
x = side of triangle that is adjacent to the angle.
y = side of triangle that is opposite to the angle.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! if angle is in Quadrant II, express the remaining trigonometric functions in terms of sin(angle).
===============
sine is positive
---
cos = sqrt(1 - sin^2) - negative
tan = sin/cos - negative
---
cot = 1/tan
sec = 1/cos
csc = 1/sin
|
|
|