Question 1116910: a curve is defined in the x-y plane by the y=(x-1)(ax^2 +bx+c) where a band c are constants. The curve torches x-axis at the point where x=1 and the line y=3x+6 at the point (-2,0).
1. find the values of a,b and c.
2. sketch the curve and on the same axes, draw the line y=3x+6, indicating clearly the points of the intersection.
3. calculate the area of the finite region bounded by the curve and the line y=3x+6
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the curve touches the x-axis at x=1, then it has a double root there. Then, since it intersects the line y=3x+6 at (-2,0), the equation for the function is
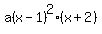
where a can be any nonzero constant.
The rest of the problem as shown can't be completed, because there was no information to use to evaluate the constant.
So to continue, I will assume the constant is 1; then the equation of the function is
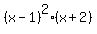
Since the description of the problem said the equation was 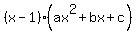 , it must be that , it must be that  . So the answers for part 1 of the problem are . So the answers for part 1 of the problem are
a=1; b=1; c=-2
Here is the graph for part 2:

The x values of the points of intersection are 0, 1-sqrt(3), and 1+sqrt(3). You can find the last two by solving the pair of equations simultaneously, knowing that one of the intersection points is at (-2,0).
I will let you do the ugly integration to find the area of the finite regions between the two curves.
|
|
|