Question 1116861: The circumference of a font wheel of a tractor Is two feet less than the circumference of a rear wheel. In traveling 3500 feet, a front wheel makes 200 more revolutions than a rear wheel. Find the circumference of each wheel.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let the circumference of the front wheel be f
since the circumference of the front wheel is 2 less than the circumference of the rear wheel, then the circumference of the rear wheel is f + 2.
let the number of revolutions that the rear wheel makes in order to travel 3500 feet be equal to x.
since the front wheel makes 200 more revolutions than the rear wheel to travel the same distance, then the number of revolutions that the front wheel makes in order to travel 3500 feet is equal to x + 200.
circumference * revolutions = distance traveled.
for the front wheel, the equation becomes 3500 = f * (x + 200)
for the rear wheel, the equation becomes 3500 = (f + 2) * x.
simplify both equations to get:
3500 = fx + 200f for the front wheel.
3500 = fx + 2x for the rear wheel.
subtract the rear wheel equation from the front wheel equation to get:
0 = 200f - 2x
solve for x to get x = 100f.
in the equation for the rear wheel, replace x with 100f to get:
3500 = fx + 2x becomes 3500 = f * 100f + 200f
this becomes 3500 = 100f^2 + 200f
subtract 3500 from both sides of the equation and flip sides to get:
100f^2 + 200f - 3500 = 0
divide both sides of this equation by 100 to get:
f^2 + 2f - 35 = 0
factor this quadratic equation to get:
(f-5) * (f+7) = 0
solve for f to get f = -7 or f = 5
f can't be negative, therefore f = 5 has to be the solution, if at all.
this means the circumference of the front wheel is 5 and the circumference of the real wheel is 7.
go back to your two original equations, which are:
3500 = f * (x + 200) for the front wheel.
3500 = (f + 2) * x for the rear wheel.
replace f with 5 in each equation to get:
3500 = 5 * (x + 200) for the front wheel.
3500 = 7 * x for the rear wheel.
solve for x in both equations to get x = 500 for both equations.
your original equation are, once again:
3500 = f * (x + 200) for the front wheel.
3500 = (f + 2) * x for the rear wheel.
when f = 5 and x = 500, these equations become:
3500 = 5 * 700 for the front wheel.
3500 = 7 * 500 for the rear wheel.
since both original equations are true, the solution looks good.
the solution is:
the circumference of the front wheel is 5 feet.
the circumference of the rear wheel is 7 feet.
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The circumference of a  front wheel of a tractor Is two feet less than the circumference of a rear wheel. front wheel of a tractor Is two feet less than the circumference of a rear wheel.
In traveling 3500 feet, a front wheel makes 200 more revolutions than a rear wheel. Find the circumference of each wheel.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is, actually, VERY SIMPLE. It can be solved and MUST BE SOLVED much simpler.
Let f be the sircumference of the front weel.
Then the circumference of the rear wheel is (f+2) ft, according to the condition.
The number of rotations of the front wheel on the distance of 3500 ft is 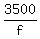 .
The number of rotations of the rear wheel on the distance of 3500 ft is .
The number of rotations of the rear wheel on the distance of 3500 ft is 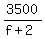 .
What the condition says about their difference, is THIS EQUATION .
What the condition says about their difference, is THIS EQUATION
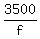 - - 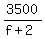 = 200.
Divide by 100 both sides. You will get = 200.
Divide by 100 both sides. You will get
 - - 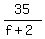 = 2.
From this point, I see the solution mentally and momentarily: f = 5.
But you can complete the solution formally in this way: multiply both sides by f*(f+2). You will get
35*(f+2) - 35f = 2f*(f+2)
35f + 70 - 35f = 2f^2 + 4f
2f^2 + 4f - 70 = 0
f^2 + 2f - 35 = 0
(f+7)*(f-5) = 0.
The only positive root f = 5 is the solution to the problem. = 2.
From this point, I see the solution mentally and momentarily: f = 5.
But you can complete the solution formally in this way: multiply both sides by f*(f+2). You will get
35*(f+2) - 35f = 2f*(f+2)
35f + 70 - 35f = 2f^2 + 4f
2f^2 + 4f - 70 = 0
f^2 + 2f - 35 = 0
(f+7)*(f-5) = 0.
The only positive root f = 5 is the solution to the problem.
Solved.
===============
To see many other similar solved problems, look in the lesson
- Challenging word problems solved using quadratic equations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Quadratic equations".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
================
When you solve any problem in Math, getting a correct solution is very important.
But presenting your solution in a good style is important, too.
In particular, I believe, that any school Math problem might be solved in 10 lines. // OK, let say, in 20 lines, with good margin.
But 40 and more lines is not a good style for the school Math problems.
|
|
|