Question 1116853: Hi tutors, this is a extra points question for a quiz, but my professor never teaches us this kind of question.
Find the exact general and particular solutions to the equation:
10sin ( 3x+ pi/6 ) + 7sqrt(3) = 2sqrt(3)
1. What is the exact general solution?
2. What is the particular solutions in {0, 2pi }
can someone help me with this question ?
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 First subtract
First subtract 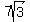 from both sides: from both sides:
 Divide both sides by 10
Divide both sides by 10

 The right side is negative.
The left side is a sine.
The sine is negative in QIII and QIV.
The 2 particular solutions in [0,2p) are,
from the unit circle 4p/3 and 5p/3.
The right side is negative.
The left side is a sine.
The sine is negative in QIII and QIV.
The 2 particular solutions in [0,2p) are,
from the unit circle 4p/3 and 5p/3.
 , , 
 , , 
 , , 
 , , 
 , , 
 The exact general solutions are found by adding 2p∙n
to the exact particular solutions in [0,2p),
where n is any integer positive, negative or 0.
So the general solutions are:
The exact general solutions are found by adding 2p∙n
to the exact particular solutions in [0,2p),
where n is any integer positive, negative or 0.
So the general solutions are:
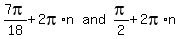 If you like you can do a little work on
those exact general solutions and get
If you like you can do a little work on
those exact general solutions and get
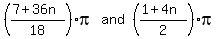 Edwin
Edwin
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. An exact general solution  . .
2. The particular solutions in   
can found by using the formula above for 
 and and  for for  , ,
 and and  for for  , and , and
 and and  for for  . .
EXPLANATION AND GRAPHICAL REORESENTATION:
As Edwin showed you, simple algebra leads you to
 . .
What angles could measure  ? ?

The angles  and and 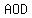 have have
 . .
One whole counterclockwise turn is  (radians), (radians),
 . .
Angles 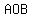 and and 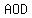 measure measure  less, and less, and  more than that, more than that,
or  and and  respectively respectively
A general formula for clockwise expression for the measure of 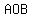 or or 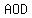 is is
 , ,
and a general formula for all angles co-terminal with those is
 for any integer for any integer  . .
So, to find the exact general solution, with  representing any integer representing any integer




RANT:
In math, there is no such a thing as "this kind of question"
or "this kind of problem".
Unfortunately, too many math instructors and tutors
classify problems into hundreds or thousands of "kinds" or "types",
and then encourage students to memorize the classification,
and the corresponding problem-solving recipes.
That makes math into a no-reasoning memorization exercise similar to learning a foreign language.
Why?
Maybe because is easier than trying to persuade students that they only need to
1) understand a few simple concepts, and
2) apply those concepts and their own brains.
Maybe because they were taught math that same way,
and they do not know any better.
Or is it that they believe the students are incapable of reasoning?
|
|
|