SOLUTION: When two balanced dice are rolled, there are 36 possible outcomes. Find the probability that thesum is a multiple of 3 or greater than 8. A. 5/12 B. 1/2 C. 13/18 D. 17/36

Wanted outcomes are 3, 6, 9, 10, 11, 12.  


3 = 1+2, or 2+1,                ====>  so there are 2 ways to get the sum of 3.


6 = 1+5, 2+4, 3+3, 4+2, or 5+1  ====>  so there are 5 ways to get the sum of 6.


9 = 6+3, 5+4, 4+5, 3+6          ====>  so there are 4 ways to get the sum of 9.


10 = 6+4, 5+5, 4+6              ====>  so there are 3 ways to get the sum of 10.


11 = 6+5 and 5+6                ====>  so there are 2 ways to get the sum of 11.


12 = 1+1                        ====>  so there is  1 way  to get the sum of 12.


Thus you have  2 + 5 + 4 + 3 + 2 + 1 = 17 wanted cases of 36 possible outcomes.


The probability under the question is 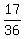 .