|
Question 1116770: Find the Coefficient of X^n in the expansion of (4-x)^4n
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Expanding the binomial power 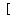 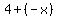 
we get 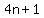 terms. terms.
Each term is a product of
a combinatorial number,
a power of  , ,
and a power of 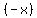 , ,
where the sum of exponents adds up to 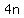 , ,
and the combinatorial number is combinations of 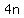
taking as many at a time as one of the exponents.
For the term in  , we get , we get  , multiplied by , multiplied by
combinations of 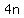 taking taking  or or 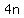 at a time, which is at a time, which is  either way. either way.
For the term in  , we get , we get  , multiplied by , multiplied by
combinations of 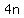 taking taking  (or (or  ) at a time. ) at a time.
You may represent combinations of 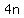 taking taking  (or (or  ) at a time by symbols such as ) at a time by symbols such as
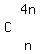 , or as , or as 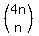 , ,
, but that combinatorial number taking  or or  , ,
is 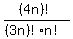  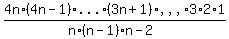 either way. either way.
So, the coefficient of 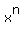 is is
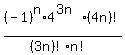  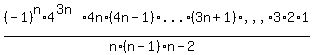
|
|
|
| |