Question 1116259: A palindrome number is a number that is the same when itís digits are reversed. Find the largest palindrome number that is the product of two 2-digit numbers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  , so a product of two two-digit numbers is at most , so a product of two two-digit numbers is at most 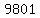 , ,
and a palindrome that is a product of two two-digit numbers is less than 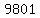 . .
The largest palindrome that is less than 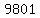 is is 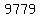 . .
If the first two digits are  and and  in that order, in that order,
the number's digit read like  , ,
and the number is a multiple of  , ,
because its value is
 . .
If that 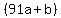 factor can be further factored as factor can be further factored as
a two-digit number  times a single digit number times a single digit number  , ,
the palindrome can be factored as the product of the two-digit numbers  and and  : :

For example, 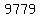 , with , with  can be factored as can be factored as
 , ,
and does not work.
If we try all possible  values for values for  , we find , we find
 . .
Out of all those values for 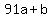 , ,
none is divisible by  , or , or  , or , or  , ,
and only two of them are divisible by  . .
That rules out all possible digit factors except  and and  , is divisible by , is divisible by  . .
So, with  , ,

is a palindrome that can be written as a product of two two-digit numbers.
There will be others, such as  , ,
but  is the largest palindrome number that is the product of two 2-digit numbers. is the largest palindrome number that is the product of two 2-digit numbers.
|
|
|