.
I don't know about the cost of producing the box, and I think that this passage is not relevant to the rest of the condition.
But I know which dimensions will minimize the surface area of the box (which directly relate to the cost of the material).
The dimensions what minimize the surface area are 15 x 15 x 15 centimeters: the box must be a cube.
It is easy to get this result analytically, using Calculus.
The surface area of the (x,y,z)-box is A(x,y,z) = 2*(xy + xz + yz).
The volume = xyz = 3375, so z = 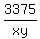 .
Therefore, A(x,y,z) =
.
Therefore, A(x,y,z) = 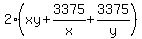 at the given volume.
The conditions
at the given volume.
The conditions 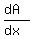 =
= 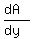 = 0 give
= 0 give
 -
- 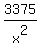 = 0 ====> x^3 = 3375 ====> x =
= 0 ====> x^3 = 3375 ====> x =  = 15, and
= 15, and
 -
- 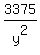 = 0 ====> y^3 = 3375 ====> y =
= 0 ====> y^3 = 3375 ====> y =  = 15.
And then z =
= 15.
And then z = 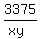 =
= 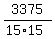 = 15.
= 15.
Solved.