Question 111606: Wha is the area of the quadrilateral with vertices at (1,1), (5,2), (4,4) and (2,3)? Put answer in square units.
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
vertices at ( , , ),( ),( , , ),( ),( , , ) and ( ) and ( , , ) )
find: the area of the quadrilateral
If
( , ,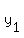 ; ;
 , ,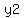 ); );
 , ,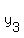 ; ;
 , ,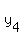
are the vertexes of the quadrilateral, the  is calculated from the formula : is calculated from the formula :

= 
= 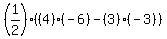
= 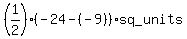
=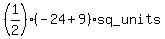
=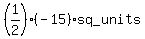
=
=
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! MathLover's SOLUTION IS INCORRECT!
`
CORRECT SOLUTION
`
by Edwin:
Wha is the area of the quadrilateral with vertices at
(1,1), (5,2), (4,4) and (2,3)? Put answer in square units.
First we draw the quadrilateral:
(1,1), (5,2), (4,4) and (2,3)
 So we must divide the quadrilateral into two triangles, for
there is a determinant formula for finding the area of a
triangle when the coordinates of the three vertices are
given:
The area of a triangle with the vertices
(x1,y1),(x2,y2), (x3,y3)
is equal to one half the absolute
value of this 3×3 determinant
|x1 y1 1|
|x2 y2 1|
|x3 y3 1|
Now we draw in either diagonal we choose, either of
these will do, either this
So we must divide the quadrilateral into two triangles, for
there is a determinant formula for finding the area of a
triangle when the coordinates of the three vertices are
given:
The area of a triangle with the vertices
(x1,y1),(x2,y2), (x3,y3)
is equal to one half the absolute
value of this 3×3 determinant
|x1 y1 1|
|x2 y2 1|
|x3 y3 1|
Now we draw in either diagonal we choose, either of
these will do, either this
 or this or this  If we use the left graph, the determinant for the
triangle with vertices (1,1), (2,3), and (4,4) is
| 1 1 1 |
| 2 3 1 | = -3
| 4 4 1 |
I am assuming you already know how to find the
value of a determinant. If you don't. then post
again asking how.
So the area of that triangle is one half of the
absolute value of -3. The absolute value of -3
is 3, and half of 3 is 1.5.
Again, using the left graph, the determinant for the
triangle with vertices (1,1), (4,4), and (5,2) is
| 1 1 1 |
| 4 4 1 | = -9
| 5 2 1 |
So the area of that triangle is one half of the
absolute value of -9. The absolute value of -9
is 9, and half of 9 is 4.5.
So the sum of the areas of those two triangles
is
1.5 + 4.5 or 6 square units of area for the
quadrilateral.
-----------------
Now let's check it by using the graph on the right
above.
If we use the graph on the right above, the
determinant for the triangle with vertices
(2,3), (4,4), and (5,2) is
| 2 3 1 |
| 4 4 1 | = -5
| 5 2 1 |
So the area of that triangle is one half of the
absolute value of -5 The absolute value of -5
is 5, and half of 5 is 2.5.
Again, using the graph on the right, the
determinant for the triangle with vertices
(2,3), (5,2), and (1,1) is
| 2 3 1 |
| 5 2 1 | = -7
| 1 1 1 |
So the area of that triangle is one half of the
absolute value of -7. The absolute value of -7
is 7 and half of 7 is 3.5.
So the sum of the areas of those two triangles
is
2.5 + 3.5 or, again, we get 6 square units of
area for the quadrilateral.
Edwin
If we use the left graph, the determinant for the
triangle with vertices (1,1), (2,3), and (4,4) is
| 1 1 1 |
| 2 3 1 | = -3
| 4 4 1 |
I am assuming you already know how to find the
value of a determinant. If you don't. then post
again asking how.
So the area of that triangle is one half of the
absolute value of -3. The absolute value of -3
is 3, and half of 3 is 1.5.
Again, using the left graph, the determinant for the
triangle with vertices (1,1), (4,4), and (5,2) is
| 1 1 1 |
| 4 4 1 | = -9
| 5 2 1 |
So the area of that triangle is one half of the
absolute value of -9. The absolute value of -9
is 9, and half of 9 is 4.5.
So the sum of the areas of those two triangles
is
1.5 + 4.5 or 6 square units of area for the
quadrilateral.
-----------------
Now let's check it by using the graph on the right
above.
If we use the graph on the right above, the
determinant for the triangle with vertices
(2,3), (4,4), and (5,2) is
| 2 3 1 |
| 4 4 1 | = -5
| 5 2 1 |
So the area of that triangle is one half of the
absolute value of -5 The absolute value of -5
is 5, and half of 5 is 2.5.
Again, using the graph on the right, the
determinant for the triangle with vertices
(2,3), (5,2), and (1,1) is
| 2 3 1 |
| 5 2 1 | = -7
| 1 1 1 |
So the area of that triangle is one half of the
absolute value of -7. The absolute value of -7
is 7 and half of 7 is 3.5.
So the sum of the areas of those two triangles
is
2.5 + 3.5 or, again, we get 6 square units of
area for the quadrilateral.
Edwin
|
|
|