Question 111596: please explain.
b^2-2bc+c^2=(b-c)^2
Found 2 solutions by stanbon, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! please explain.
b^2-2bc+c^2=(b-c)^2
----------------------
I'll show you that the right side of the equation is the
same as the left side:
--------------
(b-c)^2
=(b-c)(b-c)
= b(b-c)-c(b-c)
=b^2-bc-bc+c^2
=b^2-2bc+c^2
==============
Cheers,
Stan H.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! => these are the square of binomials:  and and 
Important to know:
If the binomial has a minus sign, then the minus sign appears  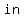 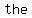 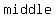 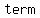 of the trinomial. of the trinomial.
If the binomial is 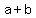 , then the middle term will be , then the middle term will be 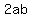 , ,
and if the binomial is 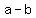 , then the middle term will be , then the middle term will be 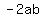 ; ;
therefore, we can use the 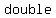  (" ("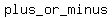 "), "),
to state the rule as follows:

The square of   produces the following three terms: produces the following three terms:
1. The square of the first term of the binomial: 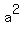
2. Twice the product of the two terms: 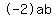
3. The square of the second term: 
The square of 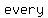 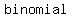 , called a perfect square trinomial, , called a perfect square trinomial,
has that form: 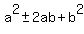 . .
So, if your square your binomial  , it will be: , it will be:

 is the square of is the square of  . .
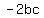 is twice the product of is twice the product of  . .
 is the square of is the square of  . .
|
|
|