|
Question 1115786: Given an ellipse: x^2/36+y^2/32=1. Determine the distance between the foci. Please explain.
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
Given an ellipse:
This is the form of an ellipse. Use this form to determine the values used to find the center along with the major and minor axis of the ellipse.
so,  ,  -> center is at ( , )= ( ,)
 ->
 ->
Find  , the distance from the center to a focus using following formula:
 or 
Find the foci:
the first focus of an ellipse can be found by adding to
.
( ,)=( ,)
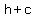the second foci
(,)=( ,)=( ,)
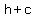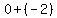the distance between the foci:
|
|
|
| |
