Question 1115426: A flare is shot upward from the edge of a 88 foot tall cliff with an initial velocity of 82 ft/sec. What is the maximum height above the ground this flare will go in feet?
Round your answer to 1 decimal place.
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a classical physics problem, and classical physics should be intuitive, because we see it in action in the world around us.
Alternatively, we can memorize "formulas" for every "type" of problem without really understanding.
THE SIMPLE/FIFTH-GRADER SOLUTION:
Somewhere in the physics book, it is stated that the acceleration of gravity increases the downward speed of an object by 32 feet per second every second:
 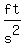 (with s as the symbol for second). (with s as the symbol for second).
So, it will take  seconds for gravity to get that initial upwards velocity down to zero, before the flare remain star having increasing downwards velocity. seconds for gravity to get that initial upwards velocity down to zero, before the flare remain star having increasing downwards velocity.
During those initial 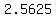 seconds the upwards velocity decreased steadily/linearly from seconds the upwards velocity decreased steadily/linearly from 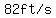 to to 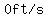 . .
 . .
During that time the average upwards velocity (in ft/s) was
 , ,
and the upwards distance covered (in feet) was
 . .
We can round that to 1 decimal place to get 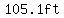 . .
As the flare started from 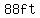 above ground, above ground,
the maximum height above the ground this flare will go (in feet) is
 . .
WITH FORMULAS (maybe your teacher wants that):
The basic formulas for an object moving in one direction with an "initial velocity"  and a constant acceleration and a constant acceleration  are are
 and and
 or or  (pick one). (pick one).
In those formulas  is distance covered, is distance covered,
 is time since a time, is time since a time,  , ,
that we can conveniently say it is the start of the observation,
an "initial velocity" is the velocity at the start of the observation,
when the velocity was  . .
From those two formulas, and your algebra skills,
you can get any other formula you will be given.
In particular, for projectiles shot upwards, from somewhere om planet Earth,
the height  above the ground is above the ground is
 , ,
where  is the initial height above the ground, and is the initial height above the ground, and  is the time since "launch". is the time since "launch".
plugging into that formula the numbers from the problem,
 . .
In algebra class, you would probably write it as
 , ,
because we like to order polynomial terms from highest to lowest exponent.
In algebra 2 courses is the US, you are likely to be told that
a quadratic function  has a maximum (if has a maximum (if 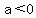 ) )
at  . If . If  it would be a minimum) it would be a minimum)
(another formula, but you do not need to memorize it if your algebra skills include "completing the square").
 is a quadratic function of is a quadratic function of  (instead of (instead of  ),with ),with  and and  , ,
so it has a maximum at  , ,
and for that value of  , in seconds, the height , in seconds, the height  , in feet, is , in feet, is
 . .
Rounding to 1 decimal place,  . .
Answer by ikleyn(52786)   (Show Source): (Show Source):
|
|
|