Question 1115011: A patient is prescribed a medication.
The patient is to take a dose of 200 mg every day at 6:00 a.m. The dose is taken by injection so that its effect is immediate.
The body processes the medication such that every 24 hours, 40% of the medication is eliminated by the body, meaning that 60% of the medication remains.
1. Create a mathematical model that will allow you to determine the amount of medicine in the body immediately after the injection each day. Make sure that your model accurately reproduces the results from the table above.
2. This medication is considered “safe” if its level in the body never exceeds 500 mg. Use your model to determine whether this medication is safe.
3. This medication becomes “effective” when its level never falls below 260 mg. On which day is this medication first considered effective. (Remember, the level is at its lowest immediately before the daily injection.
( I just need help understanding the problem, I'm not sure how to start... there's more questions to this page but there are too many. Please if I could get the basics on how to model the problems. Thank you.
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
Very 1-st day, 6:00 am after injection 200
2-nd day, 6:00 am after injection 200 + 0.6*200
3-rd day, 6:00 am after injection 200 + 0.6*200 + 0.6^2*200
4-th day, 6:00 am after injection 200 + 0.6*200 + 0.6^2*200 + 0.6^3*200
Do you see the pattern ?
For a long time "after" (many days after) the accumulated amount at 6:00 am after injection = ( approximately equal but slightly less than )
= the sum of the infinite geometric progression with the first term of 200 mg and the common ratio of 0.6 =
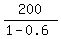=  = 200/0.4 = 500 mg.
The minimum accumulated level is the minutes BEFORE 6:00 am, before the current injection, and it is equal to
1 minute before 6:00 am of the 2-nd day 0.6*200 = 120 mg.
1 minute before 6:00 am of the 3-rd day 0.6*200 + 0.6^2*200 = 192 mg.
1 minute before 6:00 am of the 4-th day 0.6*200 + 0.6^2*200 + 0.6^3*200 = 235 mg.
1 minute before 6:00 am of the 5-th day 0.6*200 + 0.6^2*200 + 0.6^3*200 + 0.6^3*200 = 278.4 mg.
Having this model and the numbers, you are now in position to make your own conclusions.
|
|
|
