SOLUTION: Use your graphing calculator to find all degree solutions in the interval 0� &#8804; x < 360� for the following equation. sin 2x = &#8722; sqrt (3)/2

Click here to see ALL problems on Trigonometry-basics

Question 1114742: Use your graphing calculator to find all degree solutions in the interval 0� ≤ x < 360� for the following equation.
sin 2x = − sqrt (3)/2
Found 3 solutions by Theo, ikleyn, greenestamps:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
your solution, according to the following graph is:

120, 150, 300, 330 degrees.

note that -.866 on the graph is the decimal equivalent of -sqrt(3)/2 rounded to 3 decimal digits.

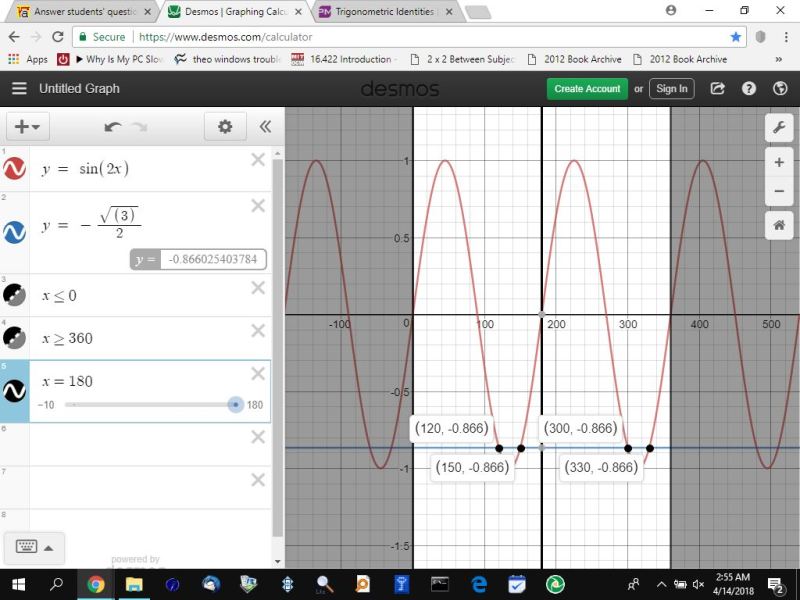
this could also be solved algebraically.

you have sin(2x) = -sqrt(3)/2.

use your calculator to find that 2x = -60 degrees.

that would be in the fourth quadrant.

the equivalent positive angle is -60 + 360 = 300 degrees.

the equivalent angle in the first quadrant is 360 - 300 = 60 degrees.

the sine is negative in the third and fourth quadrant, so your equivalent angle in the third quadrant is 240 and your equivalent angle in the fourth quadrant is 300 degrees.

you have 2x = 140 and 2x = 300.

solve for x to get x = 120 and 150.

now you need to understand frequencies and periods of the sine function.

the frequency of sin(2x) is 2.

the period is 360 / 2 = 180.

that means that sin(2x) does a full cycle in 180 degrees rather than 360 degrees.

that means that the full sine wave will repeat 2 time every 360 degrees.

you have 120 and 150 degrees.

that's the first full cycle.

the second full cycle will be 180 degrees more than 120 and 180 degrees more than 150.

that gets you to 120, 150, 300, 330 degrees.

the graph confirms this to be true.

Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website!
.

sin(2x) = ====> 2x = 240� or 2x = 300�. It implies x = 120� and x = 150�. But since your x must be in the interval 0� <= x < 360�, you must analyze 2x in the interval 0� <= 2x < 720�. In this interval, you have two more solutions for 2x. They are 2x = 240� + 360� = 600� and 2x = 300� + 360� = 660�, which implies for x x = = 300� and x = = 330� are the solutions too, in the inteval [0�,360�). So, there are 4 solutions x = 120�, 150�, 300� and 330�.

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

As you can see, there are different ways of explaining how to find all the solutions. Here is what is easiest for me....

(1) A sine value of -sqrt(3)/2 means a 60 degree reference angle in quadrant III or IV.
(2) means

So we need to find all the values of x for which 2x is an angle in quadrant III or IV with a reference angle of 60 degrees.

Angles 2x between 0 and 720 with a 60 degree reference angle in quadrant III or IV are
(a) 180+60 = 240 degrees;
(b) 360-60 = 300 degrees;
(c) 240+360 = 600 degrees; and
(d) 300+360 = 660 degrees

Then the corresponding values of x (the solutions to the given equation) are
(a) 240/2 = 120 degrees;
(b) 300/2 = 150 degrees;
(c) 600/2 = 300 degrees; and
(d) 660/2 = 330 degrees

SOLUTION: Use your graphing calculator to find all degree solutions in the interval 0� &#8804; x < 360� for the following equation. sin 2x = &#8722; sqrt (3)/2

SOLUTION: Use your graphing calculator to find all degree solutions in the interval 0� ≤ x < 360� for the following equation. sin 2x = − sqrt (3)/2