Question 1114640: Find all solutions of the equation in the interval [0, 2π). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)
8cos^3x=8cosx
Found 3 solutions by Theo, MathTherapy, Alan3354:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i find it easier to work in degrees and then convert to radians.
i can also work in radians directly, but it's not as easy because degrees are more intuitive than radians, at least to me.
what makes radians easier to work with is to not simplify the fractions, but keep them with the same denominator.
then it's easier to see what quadrant you're working in.
your equation is 8 * cos^3(x) = 8 * cos(x)
divide both sides of this equation by 8 and you get cos^3(x) = cos(x)
subtract cos(x) from both sides of this equation and you get cos^3(x) = cos(x) = 0
factor out a cos(x) and you get cos(x) * (cos^2(x) - 1) = 0
this will be true if cos(x) = 0 or if cos^2(x) - 1 = 0 or both = 0.
one answer is cos(x) = 0
the other answer starts with cos^2(x) - 1 = 0
add 1 to both sides of this equation to get cos^2(x) = 1
take the square root of both sides of this equation to get cos(x) = plus or minus 1.
you have:
cos(x) = 0
cos(x) = 1
cos(x) = -1
solve for x in each of these equations to get:
arccos(0) = 90 degrees.
arccos(1) = 0 degrees.
arccos(-1) = 180 degrees.
it helps to know your quadrants.
90 degrees can be considered to be in the first quadrant or in the second quadrant.
it's on the borderline.
assuming it's in the first quadrant, then:
comparable angle in the second quadrant is 180 - 90 = 90 degrees.
that's not surprising since it is on the border.
comparable angle in the third quadrant is 180 + 90 = 270 degrees.
comparable angle in the fourth quadrant is 360 - 90 = 270 degrees.
that's also not surprising since 270 degrees is on the border between the third and the fourth quadrant.
since cos(90) = 0 and cos(270) = 0, the sign is not important, and you can safely say that both angles give you the same trigonometric function and sign.
so far you have 90 degrees and 270 degrees that are between 0 and 360 degrees.
cos(1) = 0 degrees.
that's in the first quadrant.
in the second quadrant that's 180 - 0 = 180 degrees.
the sign of cosine in the second quadrant is negative, so that doesn't work for cos(x) = 1.
in the third quadrant that's 180 + 0 = 180 degrees.
in the fourth quadrant, that's 360 - 0 = 360 degrees.
the sign of cosine in the fourth quadrant is positive so that works.
so far, you have 90, 270, 0, 360 degrees.
arccos(-1) = 180 degrees by the calculator.
it turns out that's the only angle between 0 and 360 that has it's cosine being equal to -1.
you now have:
0, 90, 180, 270, 360 degrees.
the equivalent angles in radians would be:
0 = 0
90 = pi/2
180 = 2pi/2 = pi
270 = 3pi/2
360 = 4pi/2 = 2pi
that should round out the list.
the easiest way to solve this problem, by far, is to use a graphing calculator.
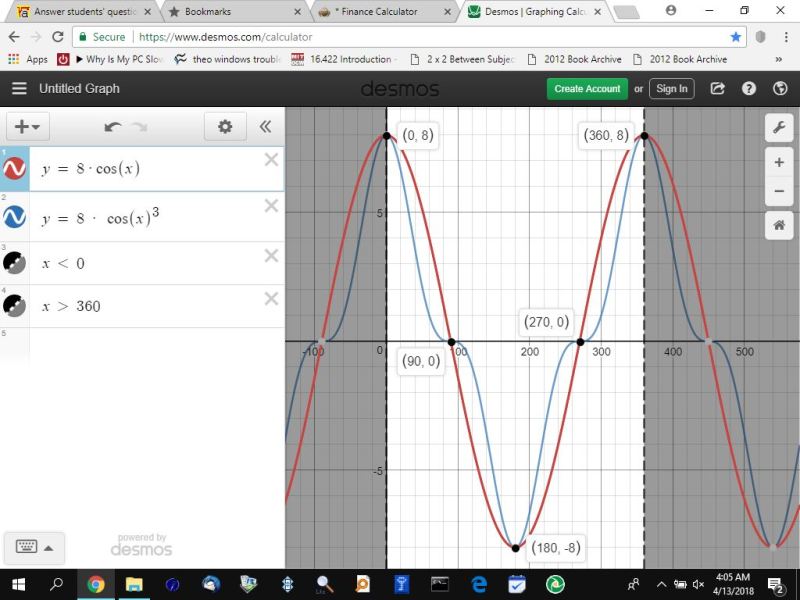
one such calculator, that is very good, can be found as www.desmos.com
using that calculator, i created two equations.
y = cos(x)
y = cos^3(x)
this is what the calculator showed me in degrees.
this is what the calculator showed me in radians.

note that, while we solved for cos(x) and cos^3(x), the actual equation was 8cos(x) and 8cos^3(x), so the amplitude of the cosine function is 8 rather than 1.
not also that cos^3(x) is shown as cos(x)^3.
in fact cos^3(x) is cos(x)^3, which is sometimes shown as (cos(x))^3.
what you are doing is taking cos(x) and then cubing it.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find all solutions of the equation in the interval [0, 2π). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)
8cos^3x=8cosx
Four (4) solutions: 
Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|