SOLUTION: Unit vector which are perpendicular to vector 2i - j - 3k and lie in the plane of vector 7i - j - k and i + 5j - 3k

Algebra ->  Vectors -> SOLUTION: Unit vector which are perpendicular to vector 2i - j - 3k and lie in the plane of vector 7i - j - k and i + 5j - 3k      Log On


   

Question 1114535: Unit vector which are perpendicular to vector 2i - j - 3k and lie in the plane of vector 7i - j - k and i + 5j - 3k
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Let A=(2,-1,-3), B=(7,-1,-1), C=(1,5,-3)
Find D that is coplanar to B and C and also perpendicular to A.
Coplanar means that
D=p%2AB%2Bq%2AC where p and q are two scalars.
.
.
.
Perpendicular means that A%2AD=0
A%2A%28pB%2BqC%29=0
2%287p%2Bq%29%2B%28-1%29%28-p%2B5q%29%2B%28-3%29%28-p-3q%29=0
%2814p%2B2q%29%2B%28p-5q%29%2B%283p%2B9q%29=0
18p%2B6q=0
3p%2Bq=0
q=-3p
So then,
D=p%2AB-3p%2AC
D=p(2,-1,-3)-3p(1,5,-3)
D=(2p,-p,-3p)+(-3p,-15p,9p)
D=(-p,-16p,6p)
To find the unit vector, divide by the magnitude of the vector,
abs%28D%29=sqrt%28%28-p%29%5E2%2B%28-16p%29%5E2%2B%286p%29%5E2%29
abs%28D%29=sqrt%28p%5E2%2B256p%5E2%2B36p%5E2%29
abs%28D%29=sqrt%28293p%5E2%29
abs%28D%29=sqrt%28293%29p
Dividing,
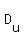D%5Bu%5D=D%2Fabs%28D%29
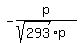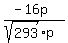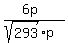D%5Bu%5D=(-p%2F%28sqrt%28293%29p%29,%28-16p%29%2F%28sqrt%28293%29p%29,%286p%29%2F%28sqrt%28293%29p%29)
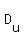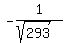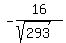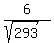D%5Bu%5D=(-1%2F%28sqrt%28293%29%29,-16%2F%28sqrt%28293%29%29,6%2F%28sqrt%28293%29%29)