Question 1114216: Mr. May invested $20,000, part at 4% and the rest at 6%. If the annual incomes from both investments were equal, find the amount he invested at each rate. Solve using two variables and a LET statement.
If it's alright, please solve by elimination. Much appreciated.
Answer by ikleyn(52905)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the amount invested at 4%, and
let y be the amount invested at 6%.
Then you have this system of 2 equations
x + y = 20000 dollars (total investment)
0.04x = 0.06y (annual incomes from both investments were equal)
Multiplying the second equation by 100 (both sides), rewrite it in THIS equivalent form
x + y = 20000 (1)
4x - 6y = 0 (2)
To apply the Elimination method, multiply eq(1) by 4 (both sides). Keep the equation (2) as is:
4x + 4y = 80000 (3)
4x - 6y = 0 (4)
Now subtract equations (4) from equation (3). The terms "4x" will cancel each other, and you will get a SINGLE equation for only one unknown
4y - (-6y) = 80000
10y = 80000 ====> y =  = 8000.
Then from eq(1) x = 20000-y = 20000-8000 = 12000.
Answer. $12000 was invested at 4% and $8000 was invested at 6%.
Check. 4% of $12000 is 0.04*12000 = 480 dollars, and
6% of $8000 is 0.06*8000 = 480 dollars, the same amount. = 8000.
Then from eq(1) x = 20000-y = 20000-8000 = 12000.
Answer. $12000 was invested at 4% and $8000 was invested at 6%.
Check. 4% of $12000 is 0.04*12000 = 480 dollars, and
6% of $8000 is 0.06*8000 = 480 dollars, the same amount.
Solved.
On the way, I showed you how the Elimination method works.
-----------------
To see many other similar solved problems on investment, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
==============
Actually, there is much simpler/easier way to solve this particular problem MENTALLY.
Since the 4% interest is the same as 6% interest, the ratio of investments is in reverse fraction:
 = =  .
I.e. x = 6 equal parts, y = 4 the same parts; in all, x+y = 6+4 = 10 parts,
and each part is .
I.e. x = 6 equal parts, y = 4 the same parts; in all, x+y = 6+4 = 10 parts,
and each part is 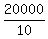 = 2000.
Thus, the 4% investment is 6 times $2000, i.e. $12000.
the 6% investment is 4 times $2000, i.e. $8000.
And you get the same answer. = 2000.
Thus, the 4% investment is 6 times $2000, i.e. $12000.
the 6% investment is 4 times $2000, i.e. $8000.
And you get the same answer.
|
|
|