Question 1114016: Find the average rate of change of the function f(x) = x ^2 + 5x + 1 over the interval
[-2, 1].
Found 2 solutions by ikleyn, rothauserc:
Answer by ikleyn(52802)   (Show Source):
You can put this solution on YOUR website! .
average rate of change of the function f(x) = x ^2 + 5x + 1 over the interval [-2,1] is equal to
 . (*)
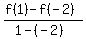Calculate f(1) and f(-2).
I hope you know how to do it. // If not, let me know . . .
Then use the expression (*).
Answer by rothauserc(4718)  (Show Source):
You can put this solution on YOUR website! the average rate of change of a function, f(x), over a closed interval [a,b] is defined as
:
(f(b) - f(a)) / (b - a)
:
our closed interval is [-2, 1], and f(x) = x ^2 + 5x + 1
:
rate of change over [-2,1] = (f(1) - f(-2)) / (1-(-2)) =
:
(7 - (-5))/3 = 12/3 = 4
:
|
|
|
