.
If sinx + cosx = -1/5, then, squaring both sides
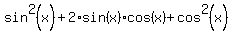 =
= 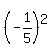 , or, replacing
, or, replacing 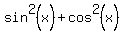 by 1
1 + 2*sin(x)*cos(x) =
by 1
1 + 2*sin(x)*cos(x) =  , and hense
2*sin(x)*cos(x) =
, and hense
2*sin(x)*cos(x) = 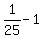 =
= 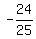 .
Since 2*sin(x)*cos(x) = sin(2x), you get
sin(2x) =
.
Since 2*sin(x)*cos(x) = sin(2x), you get
sin(2x) = 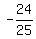 .
Next, since
.
Next, since  <= x <=
<= x <=  , you have for 2x
, you have for 2x  <= 2x <=
<= 2x <=  , i.e. 2x lies in QIV.
Therefore, cos(2x) =
, i.e. 2x lies in QIV.
Therefore, cos(2x) = 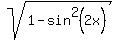 =
=  =
= 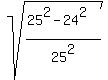 =
=  =
= 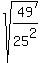 =
=  .
The sign at sqrt is "+" (plus) since cosine is positive in QIV.
Answer. cos(2x) =
.
The sign at sqrt is "+" (plus) since cosine is positive in QIV.
Answer. cos(2x) =  .
.