Question 1113953: Angles A and B are acute angles such that tanA+tanB+(tanA)(tanB)=1. If A-B=41°, find the measure of angle A.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Angles A and B are acute angles such that tanA+tanB+(tanA)(tanB)=1. If A-B=41°, find the measure of angle A.
~~~~~~~~~~~~~~~~~~
It is nice non-standard Trigonometry problem.
I will show you how to solve it.
You are given
tan(A) + tan(B) + (tan(A))*(tan(B)) = 1.
It implies
tan(A) + tan(B) = 1 - (tan(A))*(tan(B)), and, after dividing both sides by the right side
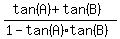 = 1.
The left side is nothing else as tan(A+B), according to the adding formula for tangent function. So your equation takes the form
tan(A+B) = 1,
and, since the angles A and B are acute, it implies that
A + B = 45 degrees.
So, now you have two equations:
A + B = 45 (1)
A - B = 41 (2)
------------------------- Add the equations to eliminate B. You will get
2A = 45 + 41 = 86 ====> A = = 1.
The left side is nothing else as tan(A+B), according to the adding formula for tangent function. So your equation takes the form
tan(A+B) = 1,
and, since the angles A and B are acute, it implies that
A + B = 45 degrees.
So, now you have two equations:
A + B = 45 (1)
A - B = 41 (2)
------------------------- Add the equations to eliminate B. You will get
2A = 45 + 41 = 86 ====> A = 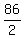 = 43.
Thus the angle A = 43°.
Then from equation (1), B = 45° - 43° = 2°.
Answer. Angle A = 43°. Angle B = 2°. = 43.
Thus the angle A = 43°.
Then from equation (1), B = 45° - 43° = 2°.
Answer. Angle A = 43°. Angle B = 2°.
Solved.
|
|
|