|
Question 1113862: A chemist needs 150 milliliters of 62% solution but has only 12% and 87% solution available . find how many milliliters of each that should be mixed to get the desired solution?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52814)   (Show Source):
You can put this solution on YOUR website! .
Let x = the amount of the 12% solution, in mL.
Then the amount of the 87% to be mixed is (150-x) mL.
The equation to find x is
0.12*x + 0.87*(150-x) = 0.62*150,
saying that the amount of the pure solvents coming with components is equal to that of the composed mixture.
Simplify and solve for x, the amount of the 12% solution.
0.12x + 0.87*150 - 0.87x = 0.62*150
-0.75x = 0.62*150-0.87*150 = (0.62-0.87)*150 = -0.25*150
x = 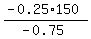 = 50.
Then the amount of the 87% solution is 150 - 50 = 100 ml.
Answer. 50 mL of the 12% solution and 100 mL of the 87% solution.
Check. 0.12*50 + 0.87*100 = 93 = 0.62*150. ! Correct !
---------------
There is entire bunch of introductory lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
- Advanced mixture problems
- Advanced mixture problem for three alloys
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Here is an alternative to the standard algebraic method for solving this kind of mixture problem that I find much faster and easier than the formal algebraic method.
The ratio in which the two ingredients must be mixed is exactly determined by where the percentage of the mixture lies between the percentages of the two ingredients.
In this problem, the percentages of the ingredients are 12 and 87; the percentage of the mixture is 62. So we find how far the percentage of the mixture is from the percentage of each ingredient: 87-62=25; 62-12=50.
The ratio of those differences is the ratio in which the two ingredients need to be mixed: 25:50 = 1:2.
Since the 62% is closer to 87% than it is to 12%, the larger part of the mixture must be the 87% ingredient.
2:1 with a total of 150ml means 100ml of the 87% and 50ml of the 12%.
The explanation with words is lengthy; but here is all that is required to solve the problem:
87-62 = 25; 62-12 = 50; 25:50 = 1:2 = 50:100 --> 50ml of 12%, 100ml of 87%
|
|
|
| |
