Question 1113653: Parallelogram ABCD is a rhombus. Side BC = 5 cm and segment AO = 3.9 cm
Parallelogram image: https://imgur.com/Kq6O5Nb
I only need
the area of ABCD,
The length of Diagonal BD,
The measure of angle d1
and the tangent ratio of angle c2.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! By definition, all sides of a rhombus have the same length.
Also, the diagonals are perpendicular bisectors of each other.
Because of that, the diagonals divide the rhombus into 4 congruent right triangles.
For each of those triangles, the hypotenuse is a rhombus side, of length  , ,
and one leg length is  . .
Applying the Pythagorean theorem we can find the other length,  : :
 . .
Solving for  , ,



 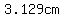
Taking one leg as the base and the other leg as the height,
the area of each triangle can be calculated as
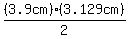 , ,
and the area of the rhombus (4 triangles) is
 
The length of diagonal BD is approximately
 , ,
or we could say it is approximately  . .
|
|
|