Question 1113541: For cosxcos3x−sinxsin3x=0, use an addition or subtraction formula to simplify the equation and then find all four solutions of the equation in the interval [0,π).
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Use the addition formula for cosine cos(a+b) = cos(a)*cos(b)-sin(a)*sin(b).
In your case, a = x, b = 3x, and the left side of your equation is cos(x+3x) = cos(4x).
Thus your equation takes the form
cos(4x) = 0,
which implies 4x =  , ,  , , 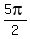 , ,  , . . .
Hence, x = , . . .
Hence, x = 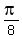 , , 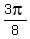 , , 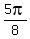 , , 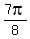 , and the rest of the roots are out of the given interval.
Answer. The solutions of the given equation in the given interval are x= , and the rest of the roots are out of the given interval.
Answer. The solutions of the given equation in the given interval are x= 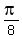 , , 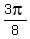 , , 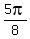 , , 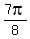 . .
---------------
On solving trigonometric equations, see the lessons
- Solving simple problems on trigonometric equations
- Solving typical problems on trigonometric equations
- Solving more complicated problems on trigonometric equations
- Solving advanced problems on trigonometric equations
in this site.
|
|
|