SOLUTION: The perimeter of a playing field for a certain sport is 282 ft. The length is 45 ft longer than width. Find the dimensions.

Algebra ->  Rectangles -> SOLUTION: The perimeter of a playing field for a certain sport is 282 ft. The length is 45 ft longer than width. Find the dimensions.      Log On


   

Question 1113407: The perimeter of a playing field for a certain sport is 282 ft. The length is 45 ft longer than width. Find the dimensions.
Found 3 solutions by josgarithmetic, ikleyn, amalm06:
Answer by josgarithmetic(39623) About Me  (Show Source):
You can put this solution on YOUR website!
2%28x%2B45%29%2B2x=282
-
x%2B45%2Bx=141
2x=141-45
2x=96
highlight%28x=48%29--------width

x%2B45=48%2B45=highlight%2893%29------length

Answer by ikleyn(52832) About Me  (Show Source):
You can put this solution on YOUR website!
.
1.   Two equations setup and solution 

2L + 2W = 282  (the perimeter),   which is simplified to  


L + W = 141,     (1)
L - W =  45.     (2)
--------------------------Add the equations to eliminate W. You will get

2L    = 141 + 45 = 186  ====>  L = 186%2F2 = 93.


Then from (1)  W = 141 - L = 141 - 93 = 48.


Answer.  The dimensions are  93 ft  and  48 ft.


1.   One equation setup and solution 

L      + W +  L     + W = 282    (perimeter)

(W+45) + W + (W+45) + W = 282

4W + 90 = 282  ====>  4W = 282 -90 = 192  ====>  W = 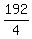192%2F4 = 48.


The same answer.


Answer by amalm06(224) About Me  (Show Source):
You can put this solution on YOUR website!
Assume the playing field has the shape of a rectangle.

Then w + w + (w + 45) + (w + 45) = 282

4w+90=282

w=48 ft, l=93 ft (Answer)

You can imagine perimeter this way: pick any edge. Then the perimeter is the distance you would have to travel around the figure to return to that point, without crossing any segment more than once.