SOLUTION: in How many ways can 5 girls any 5 boys be arranged in a row such that the 2 boys are not together.

In this problem, you can assume that all the "seats" are numbered from 1 to 10, from left to right. 


Then, under given conditions, there are only TWO major configurations:


    a)  the boys are placed at the "odd" seats;   and/or

    b)  the boys are placed at the "even" seats.


Case a) gives  5! = 120 different arrangements for boys and the same number of 5! = 120 different arrangements for girls.

In all, there are 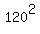   arrangements, when the boys are seating at  "odd" seats.



Case b) gives 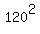   different arrangements, too (by the same arguments).


Hence, there are    arrangements, in all.