Question 1113342: A cart weighing 50 lb is placed on a ramp inclined at 15� to the horizontal. The cart is held in place by a rope inclined at 60� to the horizontal, as shown in the figure. Find the force that the rope must exert on the cart to keep it from rolling down the ramp. (Round your answer to one decimal place.)
Found 3 solutions by mananth, ikleyn, amalm06:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! We presume there is no friction then the parallel component acting along the incline is mg sin ( 15)
The rope is at an angle of ( 60- 15 ) = 45 degrees from the incline.
so the component of the force of the rope along the incline is F sin(45)
Since the cart is stationary there is equilibrium.
F sin( 45) = m * g * sin(15)
F = 50 * sin(15) / sin(45 ) lb wt
= 50 * 32 * sin(15) / sin ( 45) poundals.
sin 45 = 1/sqrt(2)
sin 15 deg =0.26
plug the values
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
The balance equation in the solution of the tutor @mananth is written I N C O R R E C T L Y.
Below find the correct solution.
The force that the rope exerts on the cart is called "rope tension", or simply "tension".
Let F be the tension.
Then it takes off F*sin(60°) from the weight W of the cart, leaving only W-F*sin(60°) as
the net vertical force acting on the cart.
This vertical force W-F*sin(60°) can be decomposed by the usual way into the sum
of two vectors/(components), one parallel to the incline and the other normal to it.
The component directed along the incline is (W-F*sin(60°))*sin(15°).
This force/(component) is balanced by the component F*cos(45°) directed along
the incline in the opposite direction.
Thus the equilibrium equation is
(W-F*sin(60°) )*sin(15°) = F*cos(45°).
which gives
F =  .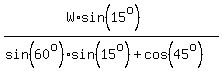
Further, sin(15°) = 0.2588;
sin(60°)*sin(15°)+ cos(45°) = 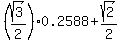 = 0.9312,
so F =  = 13.9 pounds (rounded).
Answer. The tension of the rope is 13.9 pounds.
=================
After reading the post by @amalm06, I conclude that his solution is wrong, too,
exactly in the same point where the tutor @mananth made his mistake,
i.e. in writing the balance equation.
I will not explain it again, because it was just carefully and accurately explained in details in my solution.
I advise to both tutors to read my solution attentively and to think about each its word.
---------------
I see that both of these tutors are able to solve the STANDARD problem for an incline.
But THIS problem is NON STANDARD. It differs from the standard. Therefore their knowledge do not work and are NOT ENOUGH.
Answer by amalm06(224)  (Show Source):
You can put this solution on YOUR website! 50 lb=22.68 kg
The angle between the rope and the ramp is 60°-15°=45°
For the cart to be in equilibrium, the component of the weight directed parallel to the incline and pointing downward must equal the component of the tension parallel to the incline and pointing upwards
T cos 45° = mg sin Θ
T= mg sin Θ/cos 45° = (22.68*9.8*sin 15)/cos 45° = 81.4 N (Answer)
My solution is definitely correct. Ignore the solution by Ikleyn, as it is pure nonsense. There is no normal component of the rope's tension.
|
|
|
