|
Question 1113273: In a condo complex, 2/3 of the men were married to 3/4 of the women. What is the ratio of married people to the total adult population of the condo complex? Explain how you can obtain this ration without knowing the actual number of men or women.
Found 3 solutions by ikleyn, greenestamps, amalm06:
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. From the condition,
 = = 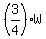 . (1)
Multiply both sides by 12. You will get
8M = 9W. (2)
or
M = . (1)
Multiply both sides by 12. You will get
8M = 9W. (2)
or
M =  (3)
2. They ask you to evaluate the ratio of (3)
2. They ask you to evaluate the ratio of  + + 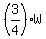 (the amount of married people) to
(M+W) (the total adult population of the condo complex).
The numerator is (the amount of married people) to
(M+W) (the total adult population of the condo complex).
The numerator is  + + 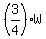 = = 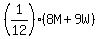 (4)
In (4), replace 8M by 9W, based on (2). Then you can continue for the numerator (4)
In (4), replace 8M by 9W, based on (2). Then you can continue for the numerator
 + + 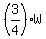 = = 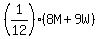 = = 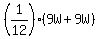 = = 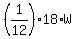 = =  .
The denominator is M + W = .
The denominator is M + W = 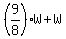 = =  . ( <<<---=== I replaced here M by . ( <<<---=== I replaced here M by  based on (3). )
3. Now the ratio under the question based on (3). )
3. Now the ratio under the question
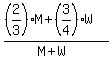 = = 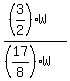 = =  = =  = =  = = 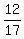 .
Answer. The ratio under the question = .
Answer. The ratio under the question = 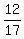 . .
Solved.
=============
The technique should not cloud / (obscure) a simple idea behind the solution.
The most general formulation of such problems is THIS:
You are given two linear forms (functions) of two variable x and y: p(x,y) = ax + by and q(x,y) = cx + dy.
You are given also linear dependence between these two variables  = e.
Then they ask you evaluate the ratio = e.
Then they ask you evaluate the ratio  .
The solution is very simple:
you express x = ey and substitute it into each of the two linear functions:
p(x,y) = ax + b*ex = (a + be)*x,
q(x,y) = cx + d*ex = (c + de)*x.
Thus each of the two functions p(x,y) and q(x,y) becomes the linear function of one variable (linear proportionality).
Then the ratio of the forms p(x,y) = ax + by and q(x,y) = cx + dy is .
The solution is very simple:
you express x = ey and substitute it into each of the two linear functions:
p(x,y) = ax + b*ex = (a + be)*x,
q(x,y) = cx + d*ex = (c + de)*x.
Thus each of the two functions p(x,y) and q(x,y) becomes the linear function of one variable (linear proportionality).
Then the ratio of the forms p(x,y) = ax + by and q(x,y) = cx + dy is
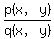 = = 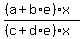 = = 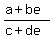 = constant not depending on x and y.
That's all. = constant not depending on x and y.
That's all.
So you actually can create/generate million of similar problems based on this technology . . .
/\/\/\/\/\/\/\/\/
The post by the tutor @amalm is W R O N G.
For your safety, simply ignore it . . .
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To be able to solve this problem, we need to assume that each marriage is between one man and one woman.
Assuming that, you need a common NUMERATOR for the two fractions. So we can say that 6/9 of the men are married to 6/8 of the women.
Then of every 17 people in the complex, there are 6 married couples; and there are 9-6=3 single men and 8-6=2 single women. That makes 12 married and 5 single people.
So the ratio of married people to the total adult population in the complex is 12:17.
Answer by amalm06(224)   (Show Source): (Show Source):
You can put this solution on YOUR website! The question does not have a unique solution. Suppose there are 30 men and 70 women. Then there are 20 married men and 42 married women. The ratio in question is 62/100. Expressed as a percentage, this turns out to be 63%. If there are 60 men and 120 women, then the ratio in question, expressed as a percentage, turns out to be 72%. Since the percentage varies, the ratio must also vary.
Note: the answer is not wrong, since the problem does not specify any constraints.
If you assume only one man marries one woman, then the problem can be solved as follows:
Let x = # of men and y = # of women
Married men: (2/3)x
Married women: (3/4)y
Since there is a one-to-one correspondence between married men & married women, (2/3)x=(3/4)y
So that y=(8/9)x
Using substitution,
Married = (2/3)x+(3/4)(8/9)x = (4/3)x
Total population: x+(8/9)x=(17/9)x
Ratio in question: (4/3)/(17/9)= 12/17 (Answer)
|
|
|
| |