SOLUTION: How can I create a "Roller Coaster" polynomial with the following requirements: - at least 3 relative maxima and/or minima - at least 2 real roots and one of the zero must have a

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: How can I create a "Roller Coaster" polynomial with the following requirements: - at least 3 relative maxima and/or minima - at least 2 real roots and one of the zero must have a      Log On


   

Question 1113152: How can I create a "Roller Coaster" polynomial with the following requirements:
- at least 3 relative maxima and/or minima
- at least 2 real roots and one of the zero must have a multiplicity of 2
- the ride length must be at least 4.5 minutes
- the ride starts at 450 feet
- the ride dives below the ground into a tunnel at least once
Thanks!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
This is not a physics problem. and a realistic roller coaster design is not expected.
You just make x=time in minutes since the start of the ride,
and 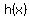h%28x%29 is the polynomial function representing height of the roller coaster car in feet as a function of time,
with a domain like [0, 4.5] for a 4.5-minute ride, or [0, 5] for a 5-minute ride.
A graphing calculator would help immensely.

The graphs of higher degree polynomials look somewhat like roller coasters.
For example, a degree 4 polynomial with a positive leading coefficient could look like this, with 2 relative minima and one relative maximum.
graph%28300%2C300%2C-1%2C9%2C-5%2C5%2C%28x-1%29%28x-2%29%28x-3%29%28x-4.5%29%29
That would satisfy the first condition "at least 3 relative maxima and/or minima".
A higher degree could give you more relative maxima and minima.

The real roots (zeros) are the points where the graph crosses the x-axis,
and if that happens for a value x=a ,
it means that 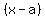%28x-a%29 is a factor of the polynomial.
The graph above shows the function f%28x%29=%28x-1%29%28x-2%29%28x-3%29%28x-4.5%29 ,
and that satisfies some of the roller coaster problem requirements.

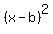If x=b is a zero of multiplicity 2, it means %28x-b%29%5E2 is a factor,
and the function is tangent to the axis at that point, but does not cross the axis.
To have a zero of multiplicity 2, you could use something like
f%28x%29=%28x-1%29%5E2%28x-3%29%28x-5%29 .
That would give you a graph that dips below the x-axis between x=3 and x=5
(the roller coaster "dives below the ground into a tunnel") once between 3 and 5 minutes),
has real roots/zeros at x=1 , x=3 , and x=5 ,
and the x=1 zero has multiplicity 2.
The graph for that is
graph%28300%2C300%2C-1%2C9%2C-10%2C10%2C%28x-1%29%5E2%28x-3%29%28x-5%29%29
In that case, the ride could end at ground level at x=5,
but maybe you do not want to end the ride at a point when the roller coaster is going up so sharply.
To end at height zero with the roller coaster going neither up nor down,
you can give the last zero multiplicity 2, as in
f%28x%29=-%28x-1%29%5E2%28x-3%29%28x-5%29%5E2 : graph%28300%2C300%2C-1%2C9%2C-15%2C35%2C-%28x-1%29%5E2%28x-3%29%28x-5%29%5E2%29 ,

or f%28x%29=-%28x-1%29%5E2%28x-3%29%28x-4.5%29%5E2 : graph%28300%2C300%2C-1%2C9%2C-15%2C35%2C-%28x-1%29%5E2%28x-3%29%28x-4.5%29%5E2%29 .
With a graphing calculator, you can try different functions to find a graph shape you like.
Maybe you would prefer f%28x%29=-%28x-1%29%5E2%28x-4%29%28x-6%29%5E2 : graph%28300%2C300%2C-1%2C9%2C-20%2C80%2C-%28x-1%29%5E2%28x-4%29%28x-6%29%5E2%29 for a 6-minute ride.
Maybe you want a higher degree polynomial for a complicated ride with more ups and downs.

The last requirement you have to meet is "the ride starts at 450 feet".
For that, you need h%280%29=450 .

For f%28x%29=-%28x-1%29%5E2%28x-3%29%28x-5%29%5E2 , f%280%29=-%28-1%29%5E2%28-3%29%28-5%29%5E2=1%2A3%2A25=75
If you multiply that function times 450%2F75=6 , you "stretch" the graph vertically, with the same general shape,
and have h%28x%29=-6%28x-1%29%5E2%28x-3%29%28x-5%29%5E2 , with h%280%29=450 .

From f%28x%29=-%28x-1%29%5E2%28x-4%29%28x-6%29%5E2 , with f%280%29=1%2A4%2A36=144 ,
multiplying times 450%2F144=3.125 you would get
h%28x%29=-3.125%28x-1%29%5E2%28x-4%29%28x-6%29%5E2 .