Question 1113107: Hello! Thank you to anyone who may be taking time out of their day to read this. I am studying Grade 12 Math online, and I am stuck on a few probability questions, (I’ll just post the first one for now to see if I catch on) and I think it’s because of how they are worded. I have noticed on some online forums that other ways to solve probabilities are by using formulas that may look like this for example: p(E)=n(E)/n(S) ...This is more advanced than my current lessons. We have been using graphing calculators to explore theoretical and experimental probabilities, and I understand the difference between the two. This assignment is on Simulation, and the Probability Statistics app on the calculator.
Create a simulation to represent the following situations:
At a horse track, Victory the Horse, has a 40% chance of winning the next 4 races. What is the probability of Victory the Horse winning at least one race?
The issue I am having, is trying to figure out what this question is asking me. Is it asking the probability of the horse winning ALL 4 races? Or once? And I think I am doing something wrong because I am getting the same calculation for both...
So the simulation I did was drawing the numbers 1-10 (numbers 1-4 represent win, 5-10 represent loss) and summoned 4 numbers (one for each race). So, the first simulation of the 4 races, she won 2/4. The second simulation she won 0/4. The third simulation she won 2/4, and so forth. I repeated 25 times until the “horse” ran 100 “races”. It turned out she won 38/100. So, 3.8/10. Is that the answer to the question? Or do I divide that by 25 to result in 1.52/4 chance of winning the 4 races???
Furthermore, if the question is asking about the probability of her winning ALL of them, would I calculate 38/100 *38/100 * 38/100 * 38/100?
I am very stumped. And the following questions are even worse. I’d just feel a lot better if I had some advice. Thank you!!
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Create a simulation to represent the following situations:
At a horse track, Victory the Horse, has a 40% chance of winning the next 4 races. What is the probability of Victory the Horse winning at least one race?
The issue I am having, is trying to figure out what this question is asking me. Is it asking the probability of the horse winning ALL 4 races? Or once? And I think I am doing something wrong because I am getting the same calculation for both...
So the simulation I did was drawing the numbers 1-10 (numbers 1-4 represent win, 5-10 represent loss) and summoned 4 numbers (one for each race). So, the first simulation of the 4 races, she won 2/4. The second simulation she won 0/4. The third simulation she won 2/4, and so forth. I repeated 25 times until the “horse” ran 100 “races”. It turned out she won 38/100. So, 3.8/10. Is that the answer to the question? Or do I divide that by 25 to result in 1.52/4 chance of winning the 4 races???
Furthermore, if the question is asking about the probability of her winning ALL of them, would I calculate 38/100 *38/100 * 38/100 * 38/100?
I am very stumped. And the following questions are even worse. I’d just feel a lot better if I had some advice. Thank you!!
======================================================================
I interpret this line:
"At a horse track, Victory the Horse, has a 40% chance of winning the next 4 races."
to mean:
Victory the horse has a 40% chance of winning ALL of her next 4 races.
(If there is any additional information to indicate this is not the case, please repost the question in its corrected form, for the rest of my answer depends on the above interpretation)
The next part I can say with relative certainty:
"What is the probability of Victory the Horse winning at least one race? "
means they want the probability of Victory winning 1, 2, 3, or 4 out of her next 4 races.
So the probabilities that must be found and added are:
P(exactly one race was won)
+ P(exactly two races were won)
+ P(exactly three races were won)
+ P(exactly four races were won)
= answer
OR,
one can compute the probability Victory loses all of her next four races and then subtract that result from 1 to get the above answer. That is:
P(winning at least once out of the next four races) = 1 - P(losing all four of the races)
——————————
I think the proper approach is as follows:
Let x = probability of Victory winning any one race of the next four races
It is given that she wins the next four races with probability 0.4:
 —> —>  —> x is approximately 0.79527073 —> x is approximately 0.79527073
This means she loses a given race with probability 1-0.79527073 = 0.20472927
The probability of Victory winning at least one race = 1 - ( probability of Victory losing all of the next 4 races) = 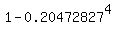 = = 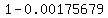 = 0.99824321 = 0.99824321
—
Answer: Victory wins at least one of her next four races with probability 
—
Sanity check: if Victory wins all four races with probability 0.4 then it is very likely she will win at least one of her next four races. This qualitatively seems right because the probability of her winning any given race is 0.79527073.
—
Similar probability calculation for further sanity checking:
Compare this to rolling a single die. The probability of rolling a number less than 6 on any given roll is 5/6. The probability of rolling a number less than 6 at least once on four rolls is 1-(1/6)^4 = 0.999228 … See how close to 1 that gets with just four rolls.
—
Further checking:
P(one race is won) = 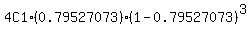 = 0.02729699 = 0.02729699
P(two races are won) = 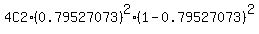 = 0.15905273 = 0.15905273
P(three races are won) = 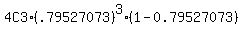 = 0.41189349 = 0.41189349
P(four races are won) = 0.4 (given, but also equal to 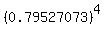 ) )
Adding them all up gives: P(one or more races won) = 0.99824321 (same as above)
——
So with my assumption of nothing omitted, and my interpretation of the question, your simulation for one race needs to use 0.79527073 (perhaps 7953/10000 is close enough) instead of 4/10, and you will need to run many more runs (say one million runs) while tracking win counts of 0, 1, 2, 3, and 4. Does that make sense?
Its late (I've been up since 5am and it is now 10pm) so I hope I didn't make any glaring errors.
——
EDIT: In the simulation, you run batches of 4 races for each of the one million runs (in all 4 million races simulated). Sorry if that wasn't clear.
|
|
|