Question 1112643: Where do I even start this problem?
Find all zeros f(x)=9x^3-3x^2-2x-4. Enter the zero separated by commas. Enter exact value, not decimal approximations.
Enter complex zeros in the form a+bi,a-bi.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website! Try Rational Roots Theorem, and look for all the possible rational roots and find any that fit, using if possible, synthetic division or polynomial division. You will only find ONE rational root. The only rational root is 1. The other possible roots to check will not be found as roots.
Next, you will just have a quadratic factor to find zeros, and you already know about general solution for a quadratic equation to find these roots. These two roots are complex.
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
Plot y = 
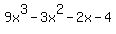In such problems, when you even don't know where to start,
start making a plot. You can do it using your calculator, or computer.
You even can find free of charge plotting software in the internet.
Having a technology in your hands, you can visualize your polynomial in 1 minute.
From the plot, you can see that x= 1 is the root.
Having this hint, you can easily confirm it making manual calculations.
Since x= 1 is the root, it means that the given polynomial is divisible by (x-1) without the remainder.
So, divide the given polynomial by (x-1). You may use long division or another technique.
After dividing, you will get a quadratic polynomial.
What to do with a quadratic polynomial, I will not explain to you. You must know it.
If you do not have technology in your hands, then the only way to find the roots is using the Rational roots theorem - or guessing.
|
|
|
