|
Question 1112498: FIND THE COORDINATES OF THE POINT EQUIDISTANT FROM (1, -6), (5, -6) AND (6, 1)
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The point under the question is the center of the circle subscribed around the triangle with the vertices at the given points.
The center of this triangle is the intersection point of any two perpendicular bisectors to the triangle sides.
So, I will search for intersection point of the two perpendicular bisectors.
Let A = (1,-6), B = (5,-6) and C = (6,1).
One side of the triangle, AB, is horizontal y= -6.
Its midpoint is D = (3,-6).
The perpendicular bisector to this segment is the line x= 3.
The side AC has the slope 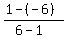 = = 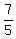 .
The midpoint of this side is E = (3.5,-2.5)
The perpendicular bisector to AC through the mid-point E has the equation
y+2.5 = .
The midpoint of this side is E = (3.5,-2.5)
The perpendicular bisector to AC through the mid-point E has the equation
y+2.5 = 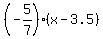 The intersection point of the two perpendicular bisectors is y+2.5 =
The intersection point of the two perpendicular bisectors is y+2.5 = 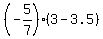 = = 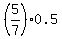 = = 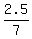 = = 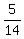 ====>
y = ====>
y = 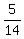 - 2.5 = - 2.5 = 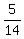 - -  = =  = = 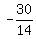 = = 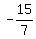 .
Answer. The point under the question is (3, .
Answer. The point under the question is (3,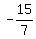 ). ).
Solved.
|
|
|
| |