Question 1112426: if f(x)=3 tan 2x, state the following.
a. the period of the function
b. the equation of any asymptotes within -pi≤x≤pi
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! if f(x)=3tan(2x), state the following.
a. the period of the function
Period = pi/2
------------------------------
b. the equation of any asymptotes within -pi≤x≤pi
x = -pi/2 and x = pi/2
------------------------
Cheers,
Stan H.
---------
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor's answer is correct about the period, but
incorrect about the vertical asymptotes.
------------------------------------------------------
The period of
  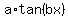 is
is 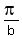 and has vertical asymptotes wherever
bx is an odd multiple of
and has vertical asymptotes wherever
bx is an odd multiple of  Therefore the period of
Therefore the period of
  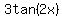 is
is  and has vertical asymptotes wherever
2x is an odd multiple of
and has vertical asymptotes wherever
2x is an odd multiple of  Odd numbers are represented by 2n-1, so
between -p and +p,
Odd numbers are represented by 2n-1, so
between -p and +p,

 Multiplying through by 4
Multiplying through by 4
 Dividing all three sides by p
Dividing all three sides by p
 Adding 1 to all three sides:
Adding 1 to all three sides:
 Dividing all three sides by 2
Dividing all three sides by 2
 And since n is an integer, n=-1,0,1,2
So when n=-1, (2n-1)pi/2 = -3p/4
And when n=1, (2n-1)pi/2 = -p/4
And when n=1, (2n-1)pi/2 = p/4
And when n=1, (2n-1)pi/2 = 3p/4
So in the interval (-p,p),
the graph continues through 4 periods, and there are 4 vertical
asymptotes at:
x = -3p/4, approximately -2.4
x = -p/4, approximately -0.8
x = p/4, approximately 0.8
x = 3p/4, approximately 2.4
the 4 green lines are the 4 vertical asymptotes:
And since n is an integer, n=-1,0,1,2
So when n=-1, (2n-1)pi/2 = -3p/4
And when n=1, (2n-1)pi/2 = -p/4
And when n=1, (2n-1)pi/2 = p/4
And when n=1, (2n-1)pi/2 = 3p/4
So in the interval (-p,p),
the graph continues through 4 periods, and there are 4 vertical
asymptotes at:
x = -3p/4, approximately -2.4
x = -p/4, approximately -0.8
x = p/4, approximately 0.8
x = 3p/4, approximately 2.4
the 4 green lines are the 4 vertical asymptotes:
 Edwin
Edwin
|
|
|