SOLUTION: for the equation y=7 times 10 to the power of 4-x, use base 10 logs to rearrange this equation to make x the subject

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: for the equation y=7 times 10 to the power of 4-x, use base 10 logs to rearrange this equation to make x the subject       Log On


   

Question 1112415: for the equation y=7 times 10 to the power of 4-x, use base 10 logs to rearrange this equation to make x the subject

Found 2 solutions by josgarithmetic, Theo:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
y=7%2A10%5E%284-x%29

-
log%28%28y%29%29=log%28%287%2A10%5E%284-x%29%29%29

log%28%28y%29%29=log%28%287%29%29%2B%284-x%29%2Alog%28%2810%29%29

Since in base 10,
log%28%28y%29%29-log%28%287%29%29=%284-x%29%2A1

log%28%28y%29%29-log%28%287%29%29=-x%2B4
log%28%28y%29%29-log%28%287%29%29-4=-x
highlight%28x=log%28%287%29%29-log%28%28y%29%29%2B4%29
OR
highlight%28x=log%28%287%2Fy%29%29%2B4%29

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
start with:

y = 7 * 10 ^ (4-x)

take the log of both sides of this equation to get:

log(y) = log(7 * 10^(4-x))

since log(a * b) = log(a) + log(b), this equation becomes:

log(y) = log(7) + log(10^(4-x))

since log(a^b) = b*log(a), this equation becomes:

log(y) = log(7) + (4-x) * log(10)

since log(10) = 1, this equation becomes:

log(y) = log(7) + 4 - x

add x to both sides of the equation and subtract log(y) from both sides of the equation to get:

x = log(7) + 4 - log(y)

if you wanted to simplify this as far as it will go, then you would get:

x = 4.84509804 - log(y)

x is now the subject of the equation.

to see if this is correct, take any value of y and place it in the equation.

any value of y > 0 should do.

i chose y = 15,000,000.

in the equation of x = log(7) + 4 - log(y), replace y with 15,000,000 to get:

x = log(7) + 4 - log(15,000,000).

do not include the commaas when you use your calculator to solve this.

this results in x = -2.330993219

now go back to the original equation of y = 7 * 10 ^ (4-x) and replace x with -2.330993219 to get:

y = 7 * 10 ^ (4 - (-2.330993219)).

this results in y = 15,000,000

the two equations are equivalent.

one solves for y.
the other solves for x.

these two equations are identical.

if you graphed both these equations, they would draw the same curve on the graph.

here's the graph of both equations and the intersection of y = 15,000,000 with x = -2.330993219.

$$$

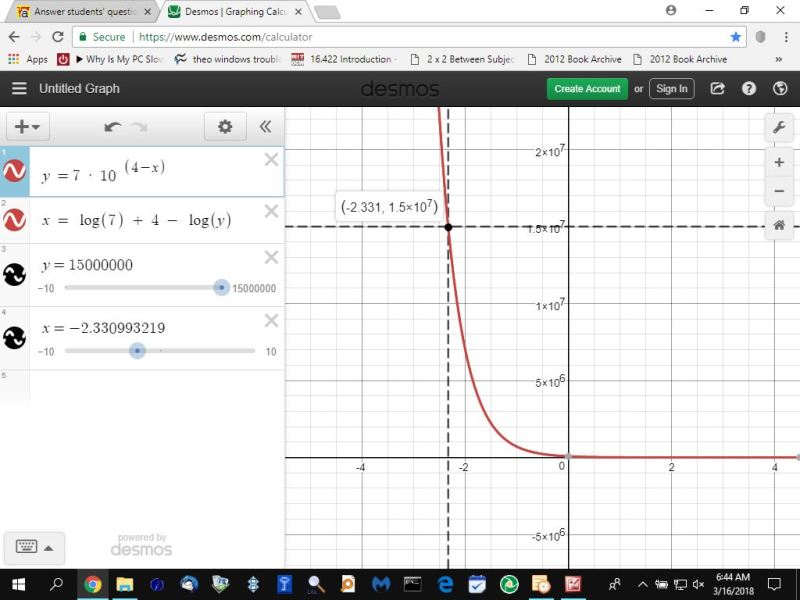
you can see that both equations draw the same graph.

you can see that the intersection of y = 15,000,000 with the graph is at the point (-2.331,15,000,000).

-2.331, shown as the x-coordinate of the intersection on the graph, is a rounded version of -2.330993219.

1.5 * 10^7, shown as the y-coordinate of the intersection on the graph, is equal to 15,000,000 in standard decimal form.